Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

( x + 3)( x + 1)( x − 5) < 0.

Ответ. x < −3, −1 < x < 4, 4 < x < 5.

Пример 3.Решить неравенство

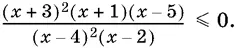
(3)

Данное неравенство не удовлетворяется в тех точках, где множители, стоящие в знаменателе, обращаются в нуль ( x = 4, x = 2). Поэтому исключим эти точки из дальнейшего рассмотрения, обозначив их на рис. 10.6 светлыми кружками.

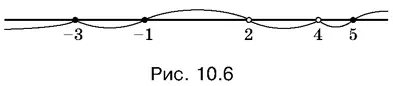
В точках же, в которых обращается в нуль числитель ( x = −3, x = −1, x = 5), неравенство превращается в равенство, т. е. эти точки должны войти в решение неравенства (3). Отметим их на рисунке черными кружками [8] Если какая-то точка уже была отмечена светлым кружком, то изменять обозначение не следует. ).

Множители ( x + 3)² и ( x − 4)², не меняющие знака на всей числовой оси, можно опустить, так как их влияние уже учтено. Во всех остальных точках неравенство (3) равносильно такому:

( x + 1)( x − 5)( x − 2) < 0.

Ответ. x ≤ −1, 2 < x < 4, 4 < x ≤ 5.

Решите неравенства:

4.(5 − 2х)(3 − x)³(x − 4)² < 0.

5.

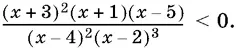
Иррациональные неравенства.Решая уравнения, мы можем получать следствия данного уравнения и закончить решение проверкой, которая отсеивает посторонние корни. При решении же неравенств обычно получаются целые интервалы решений, что сильно усложняет проверку. Поэтому неравенства преобразовывают так, чтобы не нарушалась равносильность.

Начнем с иррациональных неравенств.

Пример 4.Решить неравенство

(4)

Нередко предлагают такое «решение»:

x ² − 55 х + 250 < ( x − 14)²,

−55х + 250 < −28 х + 196,

x > 2,

которое обосновывают следующим образом: «Левая часть меньше правой, но неотрицательна, так как мы имеем дело с арифметическим корнем. Следовательно, обе части данного неравенства неотрицательны, и его можно возвести в квадрат, не нарушая равносильности неравенства».

Чтобы убедиться, что неравенство решено неверно, подставим в данное неравенство, например, x = 10.

Проанализируем ход приведенных здесь рассуждений. Они доказывают, что если неравенство (4) удовлетворяется при некоторых x , то обе части его можно возвести в квадрат, и тогда x > 2. Однако отсюда не следует обратное, что исходное неравенство удовлетворяется при всех x > 2.

Присутствие в неравенстве (4) квадратного корня накладывало на неизвестное определенные ограничения, которые оказались разрушенными после возведения неравенства (4) в квадрат.

Трехчлен x ² − 55 х + 250 вначале стоял под знаком квадратного корня, а потому должен был быть неотрицательным. После возведения неравенства (4) в квадрат это ограничение исчезло; теперь ничто не мешает трехчлену стать отрицательным. Даже наоборот, в этом случае неравенство x ² − 55 х + 250 < ( x − 14)² удовлетворяется наверняка, так как справа стоит величина, которая не может стать меньше нуля.

Чтобы подкоренное выражение оставалось неотрицательным, мы должны добавить к полученному после возведения в квадрат неравенству требование x ² − 55 x + 250 ≥ 0, т. е. x ≤ 5, x ≥ 50. Из полупрямой x > 2 оказались выделенными две ее части: 2 < x ≤ 5, x ≥ 50.

Но и теперь еще не все. Достаточно подставить в исходное неравенство значение x = 4, и мы убедимся, что оно не удовлетворяется. Дело в том, что при возведении в квадрат мы устранили еще одно ограничение, которое присутствовало в неравенстве (4). В левой части первоначального неравенства стоит квадратный корень, т. е. неотрицательное число. Чтобы это неравенство удовлетворялось, правая его часть x − 14 должна быть больше нуля. Итак, надо добавить ограничение x − 14 > 0, которое присутствовало в исходном неравенстве и оказалось разрушенным после возведения в квадрат.

Таким образом, после возведения данного неравенства в квадрат, мы должны позаботиться о сохранении всех ограничений, которые присутствуют в данном неравенстве. Неравенство (4) нужно было заменить системой

решая которую мы нашли бы, что

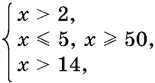
т. е. x ≥ 50.

В каждом из неравенств 6—9 освободитесь от иррациональности, не нарушая равносильности:

6.

7.

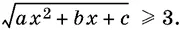
8.

9.

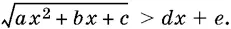
Показательные и логарифмические неравенства.При решении показательных и логарифмических неравенств пользуются следующими свойствами:

1. Неравенство f ( x ) φ( x )> 1, где f ( x ) > 0, равносильно совокупности двух систем неравенств:

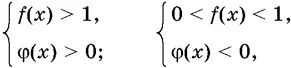
или системе неравенств

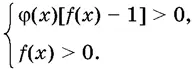
1а. Неравенство f ( x ) φ( x )< 1, где f ( x ) > 0, равносильно совокупности двух систем неравенств:

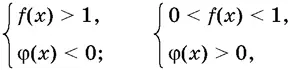
или системе неравенств

2. Неравенство log f ( x )φ( x ) > 0 равносильно совокупности двух систем неравенств:

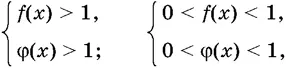
или системе неравенств

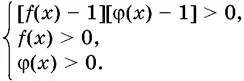
2а. Неравенство log f ( x )φ( x ) < 0 равносильно совокупности двух систем неравенств: