Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Что же касается проверки, то она оказывается излишней только в тех случаях, когда исследована эквивалентность применявшихся в процессе решения преобразований.

Для этого необходимо выяснить, при каких преобразованиях мы получаем следствие данного уравнения, а в каких случаях нам грозит потеря корней.

Посмотрим на примере, как исследуется равносильность двух уравнений. Имеет место следующая теорема.

Теорема 1.Если в уравнении произвести уничтожение двух подобным членов, то получится следствие данного уравнения.

Другими словами, если уравнение

f ( x ) + φ( x ) − φ( x ) = 0 (4)

заменить уравнением

f ( x ) = 0, (5)

то потери корней не произойдет, а приобретение корней может произойти.

Сначала докажем, что не произойдет потери корней, т. е. что любой корень x = с уравнения (4) является корнем уравнения (5). Если x = с — корень уравнения (4), то

f ( с ) + φ( c ) − φ( c ) = 0 (4′)

— истинное числовое равенство, где f ( с ) и φ( с ) — числа. Оно не нарушится в результате прибавления и последующего вычитания числа φ( c ).

Таким образом,

f ( с ) = 0 (5′)

— истинное числовое равенство, т. е. x = с является также и корнем уравнения (5).

Остается убедиться в том, что уравнение (5) может иметь корни, посторонние для уравнения (4). Чтобы доказать это, достаточно привести пример. Уравнение

cos x + tg x − tg x = 0 (4′′)

после уничтожения подобных членов принимает вид

cos x = 0. (5′′)

Корнями уравнения (5′′) будут числа x = π/ 2+ k π. Но ни одно из них не удовлетворяет уравнению (4′′), так как tg x перестает существовать, когда cos x = 0.

Итак, теорема доказана.

Несколько уравнений могут образовать систему или совокупность.

Говорят о системе уравнений, если требуется найти все решения, общие для всех уравнений, входящих в систему.

Если же нужно найти все такие решения, которые удовлетворяют хотя бы одному из нескольких уравнений, то говорят, что эти уравнения образуют совокупность.

Систему уравнений обычно записывают в столбик и ставят сбоку фигурную скобку — знак системы; совокупность уравнений, как правило, записывается в строку. Если же совокупность уравнений удобнее записать в столбик, то слева ставят квадратную скобку — знак совокупности.

Если мы рассмотрим совокупность двух уравнений:

x ² − x − 2 = 0 и x ² − 2 x − 3 = 0,

то корни первого: x 1= 2, x 2= −1 нужно объединить с корнями второго: x 1= 3, x 2= −1. Получим решение совокупности:

x 1= 2, x 2= −1, x 3= 3.

Если же мы рассмотрим систему

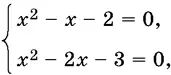
то из корней первого уравнения нужно выбрать те, которые удовлетворяют и второму уравнению системы. Получим только одно решение системы: x = −1.

Уравнение

f ( x ) · φ( x ) = 0 (6)

называется распадающимся.

Теорема 2.Уравнение (6) равносильно совокупности двух систем :

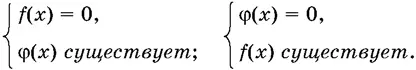
(7)

Доказательство.Если x = а — корень уравнения (6), то f ( а ) и φ( а ) существуют и либо f ( а ) = 0, либо φ( а ) = 0 (случай, когда оба сомножителя одновременно равны нулю нами из рассмотрения не исключен). Следовательно, одна из систем (7) удовлетворяется при x = а .

Пусть теперь x = а — корень совокупности (7). Если при x = а удовлетворяется либо первая, либо вторая система, то и в том и в другом случае f ( x ) · φ( x ) = 0, т. е. x = а — корень уравнения (6).

Докажите следующие теоремы о равносильности уравнений.

17.Если к обеим частям уравнения

f ( x ) = φ( x )

прибавить выражение ψ( x ), то в случае, когда ψ( x ) имеет смысл при всяком x , получится равносильное уравнение, в противном случае могут быть потеряны корни.

18.Уравнения

f ( x ) + ψ( x ) − ψ( x ) = φ( x )

и

f ( x ) = φ( x )

в случае, когда ψ( x ) имеет смысл при всяком x , равносильны; в противном случае второе уравнение является следствием первого.

19.Если в уравнении

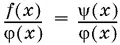
(8)

отбросить знаменатель, то получится уравнение

f ( x ) = ψ( x ),

являющееся следствием данного уравнения.

19а.Уравнение (8) равносильно системе

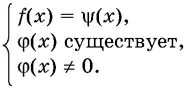
(8а)

20.Если обе части уравнения f ( x ) = φ( x ) возвести в квадрат, то полученное уравнение

[ f ( x )]² = [φ( x )]² (9)

является следствием данного уравнения. Уравнение (9) равносильно совокупности двух уравнений:

f ( x ) = φ( x ), f ( x ) = −φ( x ).

21.Чему равносильна система

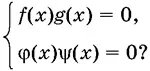
22.Докажите, что следствием уравнения

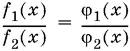
является уравнение

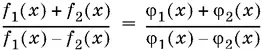
при условии, что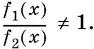

Найдите действительные корни уравнений:

9.1.| x | − 2| x + 1| + 3| x + 2| = 0.

9.2.| x ² − 9| + | x ² − 4| = 5.

9.3.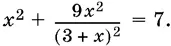

9.4.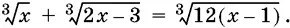

9.5.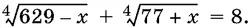

9.6.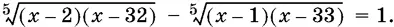

9.7. 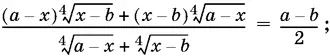а и b — действительные числа.

9.8. 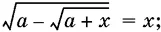а — действительное число.

9.9. а — действительное число.