Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

8.6.Найдите все целочисленные решения уравнения

2 x ² у ² + у ² − 6 x ² − 12 = 0.

8.7.В уравнении

x 4+ аx ³ + bx ² + 6 x + 2 = 0

один из корней равен √3 + 1. Найдите остальные корни уравнения, если а и b — рациональные числа.

8.8.При каких значениях а оба корня уравнения

x ² − ( а + 1) x + а + 4 = 0

отрицательны?

8.9.Найдите соотношение между а , b и с , если корни уравнения

x ³ + аx ² + bx + с = 0

образуют геометрическую прогрессию.

8.10.Известно, что уравнение x ³ + px + q = 0 имеет корни α 1, α 2, α 3. Выразите сумму α 1² + α 2² + α 3² через p и q .

8.11.При каких а и α трехчлен х ³ + ax + 1 делится на двучлен x − α без остатка и частное от деления при всех x больше нуля?

8.12.Остатки от деления многочлена относительно x на x − 2 и x − 3 равны соответственно 5 и 7. Найдите остаток от деления этого многочлена на ( x − 2)( x − 3).

8.13.Найдите все действительные значения p и q , при которых х 4+ 1 делится на x² + рх + q .

8.14.Докажите, что многочлен

x² n + 1 − (2 n + 1) х n + 1+ (2 n + 1) х n − 1,

где n — натуральное число, делится на ( x − 1)³.

8.15.Определите p и q так, чтобы многочлен

6 х 4 − 7 х ³ + рх ² + 3 х + 2

делился без остатка на x² − x + q .

Равенства. Тождества.Два математических выражения, соединенных знаком =, образуют равенство .

Примеры равенств:

а ² + b ² = с ², 3 = 3, 3 = 5,

sin² x + cos² x = 1, 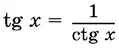, sin x = 3.

Числовое равенство может быть истинным (верным) или ложным (неверным). Равенство 3 = 3 истинное, равенство 3 = 5 ложное.

Буквенное равенство при различных значениях входящих в него букв также принимает одно из двух значений: «истина» или «ложь». Например, равенство а ² + b ² = с ² при а = 3, b = 4, с = 5 истинно, а при а = 3, b = 4, с = 6 ложно. Равенство sin² x + cos² x = 1 истинно при всех действительных значениях x , а равенство sin x = 3 всегда ложно.

Если какая-либо часть равенства (или обе части одновременно) перестает существовать, то равенство становится ложным. Равенство 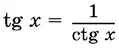ложно при 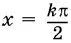, где k — любое целое число, так как для четных k не существует ctg x , а для нечетных k не существует tg x . Равенство ложно при x = −1, так как его левая часть теряет смысл при этом значении x (обратите внимание, что правая часть существует всегда). Обе части равенства sin x = 3 всегда имеют смысл, однако это равенство всегда ложно.

Для любого математического выражения можно указать множество систем (наборов) значений входящих в него букв, при которых это выражение существует , т. е. принимает некоторое числовое значение. Такое множество мы будем называть областью определения ( областью существования ) рассматриваемого математического выражения.

Для выражения 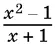областью определения является числовая ось с «выколотой» точкой x = −1.

Для выражения log у √ x найти область определения уже несколько сложнее. Во-первых, из числа x извлекается квадратный корень. Эта операция возможна, если x ≥ 0. Чтобы затем можно было найти логарифм от √ x , необходимо √ x > 0. Оба условия выполняются при x > 0. В основании логарифма может стоять лишь положительное число, отличное от единицы. Таким образом, получаем область определения: x > 0, у > 0, у ≠ 1.

Два математических выражения называются тождественными , если

1) их области определения совпадают;

2) они принимают одинаковые числовые значения при подстановке в каждое выражение одного и того же набора значений входящих в него букв, произвольно выбранного из области определения.

Равенство, в котором правая и левая части являются тождественными выражениями, называется тождеством .

Для обозначения тождественного равенства иногда используется символ ≡.

Примеры тождеств: ( а − b )² = а ² − 2 аb + b ², sin² x + cos² x = 1,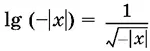

Первые два тождества общеизвестны. Последнее равенство тоже является тождеством. В самом деле, область определения левой части не содержит ни одной точки, область определения правой части тоже не содержит ни одной точки. Поскольку области определения правой и левой частей — пустые множества, то требования 1) и 2) в определении тождества удовлетворяются. Равенство 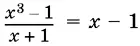, как мы видели, истинно при всех x , кроме x = −1. Оно не является тождеством, так как требование 1) не удовлетворено. Однако нарушение происходит только в одной точке.

Введем понятие неабсолютного тождества.

Пусть в нашем распоряжении есть два математических выражения, имеющих разные области определения. Обозначим через U их общую часть. Если на множестве U значения обоих математических выражений совпадают, то говорят, что они неабсолютно тождественны , а соответствующее равенство называют неабсолютным тождеством .

Характерным примером неабсолютного тождества является соотношение

lg ху = lg x + lg у .

Область определения правой части: x > 0, у > 0, т. е. все точки плоскости, лежащие внутри I квадранта. Область определения левой части: x > 0, у > 0; x < 0, у < 0; это уже будут внутренние точки I и III квадрантов. Общая часть областей определения: x > 0, у > 0. На этой общей части приведенное соотношение превращается в истинное равенство.

Напомним определение тождества, которым обычно пользуются в средней школе.

Тождеством называется равенство, справедливое при всех значениях входящих в него букв, при которых обе его части имеют смысл.