Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

4.6.Дан куб ABCDА 1 В 1 С 1 D 1. На продолжении ребер AB , АА 1, AD отложены соответственно отрезки ВР , А 1 Q , DR длины 1,5 АВ . Через точки P , Q , R проведена плоскость. В каком отношении эта плоскость делит объем куба?

4.7.Площадь боковой грани правильной шестиугольной пирамиды равна Q . Вычислите площадь сечения, проходящего через середину высоты пирамиды параллельно боковой грани.

4.8.В треугольной призме ABCА 1 В 1 С 1боковое ребро равно l . В основании призмы лежит правильный треугольник со стороной b , а прямая, проходящая через вершину В 1и центр основания ABC , перпендикулярна к основаниям. Найдите площадь сечения, проходящего через ребро AB и середину ребра СС 1.

4.9.В прямоугольном параллелепипеде ABCDА 1 В 1 С 1 D 1( ABCD и А 1 В 1 С 1 D 1— основания) даны длины ребер AB = а , АD = b , АА 1= с . Пусть точка O — центр основания ABCD , O 1— центр основания А 1 В 1 С 1 D 1, F — точка, делящая отрезок O 1 O в отношении 1 : 3. Найдите площадь сечения данного параллелепипеда плоскостью, проходящей через точку F параллельно его диагонали АС 1и диагонали ВD основания.

4.10.В точке E , находящейся на расстоянии 2 h от плоскости основания куба с ребром h и на расстоянии R > 2 h от прямой, соединяющей центры оснований куба, помещен источник света. Докажите, что тень, отбрасываемая кубом на плоскость основания, будет иметь наибольшую площадь, когда плоскость, проходящая через центр куба, точку E и одну из вершин, перпендикулярна к плоскости основания.

4.11.На плоскость Π под прямым углом к ней падает пучок параллельных лучей. Как расположить над плоскостью куб с ребром а , чтобы отбрасываемая им тень имела максимальную площадь? Найдите площадь максимальной тени.

5.1.Найдите геометрическое место оснований перпендикуляров, опущенных из центра O круга на хорды, проходящие через данную точку N внутри круга.

5.2.На плоскости зафиксированы две различные точки А и В . Найдите геометрическое место точек M , для каждой из которых AM · ВМ · cos ∠ AMB = ¾ АВ ².

5.3.На плоскости зафиксированы две различные точки А и В . Докажите, что геометрическое место точек M , удовлетворяющих условию 2 АМ ² + МВ ² = АВ ², есть окружность с диаметром AC , где точка С лежит на отрезке AB , причем AC / BC = 2.

5.4.Дан треугольник ABC . Найдите геометрическое место точек M , таких, что площади треугольников АМВ и NМС равны.

5.5.На плоскости даны два отрезка: AB и CD . Найдите геометрическое место точек M плоскости, для которых площади треугольников ABM и CDM равны.

5.6. Дан куб с ребром а . Найдите геометрическое место середин отрезков длины l , один из концов которых лежит на диагонали верхнего основания, а другой — на непараллельной ей диагонали нижнего основания.

6.1.Докажите, что р ² − 1 делится на 24, если p — простое число, большее 3.

6.2.Докажите, что n ³ + 2 n при любом натуральном n делится на 3.

6.3.Докажите, что число 3 105+ 4 105делится на 49 и 181.

6.4.Сколько в числе 500! содержится множителей 2?

6.5.Делится ли число 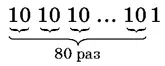на 81?

6.6.Определите, при каких целых значениях n выражение n 4+ 4 является простым числом.

6.7.Докажите, что 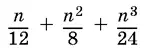является целым числом при любом четном n .

6.8.При каких целых значениях x дробь 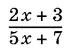сократима?

6.9.Найдите все пятизначные числа вида 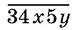( x — цифра сотен, y — цифра единиц), которые делятся на 36.

6.10.Найдите трехзначное число 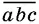( а , b , с — его цифры), если четырехзначное число 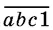в три раза больше четырехзначного числа .

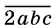6.11.Найдите простое число p , если p + 2 и p + 4 — простые числа.

6.12.Докажите, что tg 5° — число иррациональное.

6.13.Найдите два последовательных натуральных числа, сумма цифр каждого из которых делится на 11.

6.14.Найдите все целочисленные решения уравнения

3 x ² − 16 xy − 35 y ² + 17 = 0.

6.15.Сколько различных целочисленных пар ( x , y ) удовлетворяют уравнению

x ² = 4 y ² + 20 025?

6.16.Найдите натуральные x и y , удовлетворяющие условию 113 x − 69 y = 11, сумма которых x + y принимает наименьшее значение.

Следующие ниже замечания относятся не только к этой главе, они имеют более общий характер.

Множества точек x числовой оси, удовлетворяющих неравенствам

1) а < x < b ;

2) а ≤ x ≤ b ;

3) а ≤ x < b ;

4) а < x ≤ b ;

5) x > а ;

6) x < а ;

7) x ≥ а ;

8) x ≤ а ,

где а < b , называются интервалами и обозначаются соответственно (а, b); [а, b]; [а, b), (а, b]; (а, +∞); (−∞, а); [а, +∞); (−∞, а].

Интервалы 1), 5) и 6) называются открытыми ; интервал 2) называется замкнутым; интервалы 3), 4), 7) и 8) называются полуоткрытыми . Иногда вместо терминов: открытый интервал, замкнутый интервал, полуоткрытый интервал используют соответственно термины: промежуток (или интервал ), отрезок (или сегмент ), полуотрезок .

По определению

Для арифметического корня имеет место формула

√ а ² = | а |.

Иногда приходится пользоваться формулами куба суммы и разности чисел в виде

( а + b )³ = а ³ + b ³ + 3 аb ( а + b );

( а − b )³ = а ³ − b ³ − 3 аb ( а − b ).