Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

Следующая формула называется формулой сложного радикала:

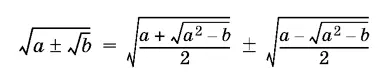
(все подкоренные выражения должны быть неотрицательными).

По определению

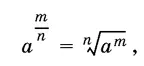
где а ≥ 0, m, n — натуральные числа и корень арифметический.

Из этого определения следует, что степени с отрицательным основанием и дробным показателем считаются не имеющими смысла . Например, 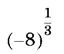не имеет смысла, в то время как .

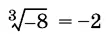По определению

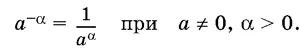
По определению

α 0= 1 при а ≠ 0.

Чтобы избежать недоразумений, удобно договориться, что знак корня используется либо для обозначения арифметического корня из неотрицательного числа, либо отрицательного корня нечетной степени из отрицательного числа.

Таким образом, .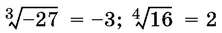

Для арифметических корней и корней нечетной степени из отрицательных чисел справедливо правило умножения и деления корней :

Правило, в силу которого показатель корня и показатель подкоренного выражения можно умножить на одно и то же натуральное число, справедливо для арифметических корней и не справедливо для корней нечетной степени из отрицательных чисел.

Замечание . В качестве показателя корня используются только натуральные числа. Иногда встречаются задачи, где показатели — достаточно сложные алгебраические выражения. Во избежание путаницы лучше знак корня в таких задачах не использовать, а прибегать к дробным показателям степени.

7.1.Упростите выражение

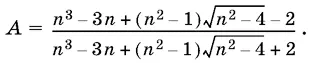
7.2.Упростите выражение

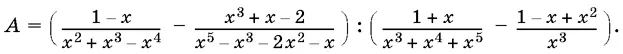
7.3.Упростите выражение

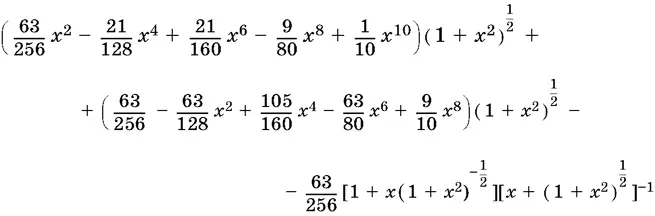
После упрощения выражения определите его знак в зависимости от x .

7.4.Упростите выражение

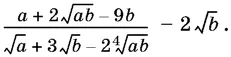
7.5.Упростите выражение

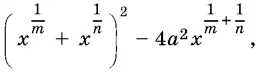
где .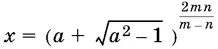

7.6.Вычислите значения выражения

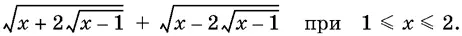
7.7.Преобразуйте выражение

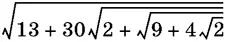
так, чтобы оно не содержало сложных радикалов.

7.8.Разложите на линейные относительно x , у , z , u множители выражение

( xy + zu )( x² − y ² + z ² − u ²) + ( xz + yu )( x² + у ² − z ² − u ²).

7.9.Докажите, что

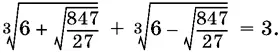
7.10.Докажите, что если а + b + с = 0, то

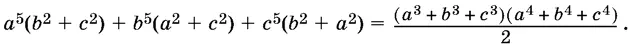
7.11.Докажите, что при всех действительных значениях x и у имеет место равенство

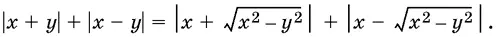
7.12.Докажите, что

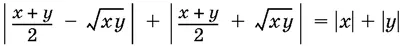
для любых действительных x и у , имеющих одинаковые знаки.

7.13. Докажите, что из условия

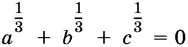
следует

( а + b + с )³ = 27 аbс .

7.14.Квадратный трехчлен 24 х ² + 48 x + 26 есть разность кубов двух линейных функций с положительными коэффициентами. Найдите эти функции.

Многочлен S ( x ) называется частным , а многочлен R ( x ) — остатком от деления многочлена P ( x ) на многочлен Q ( x ), если равенство

P ( x ) = Q ( x ) · S ( x ) + R ( x )

является тождеством и степень многочлена R ( x ) меньше степени многочлена Q ( x ).

Обобщенная теорема Виета.Для корней х 1, х 2, ..., х nуравнения

а 0 х n + a 1 x n − 1+ ... + а n − 1 x + а n = 0

имеют место формулы:

,

,

.

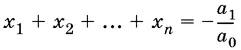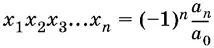Для уравнения a 0 x n + a 1 x n − 1+ ... + а n = 0 с целыми коэффициентами а 0, а 1, ... , а n верна теорема: если уравнение имеет рациональный корень p/ q , то p числитель является делителем свободного члена а n, а знаменатель q — делителем коэффициента а 0.

В частности, если а 0= 1, то уравнение может иметь только такие целые корни, которые являются делителями свободного члена а n .

8.1.Решите уравнение

( x − 4,5) 4+ ( x − 5,5) 4= 1.

8.2.Решите уравнение

(4 x + 1)(12 x − 1)(3 x + 2)( x + 1) = 4.

8.3.Докажите, что уравнение

x ² − 3 у ² = 17

не имеет решений в целых числах.

8.4.Найдите все целые решения уравнения

x ² − 6 xу + 13 у ² = 100.

8.5.Найдите остаток от деления многочлена x 99+ x ³ + 10 x + 5 на многочлен x ² + 1.