Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

log x + log у = log xу

не приводит к потере корней. Если же по ходу преобразований возникла необходимость прологарифмировать произведение, то нужно воспользоваться другим неабсолютным тождеством

log xу = log | x | + log | у |,

применение которого может лишь расширить область определения уравнения.

Есть второй прием, позволяющий избежать потери решений, который мы поясним на примере уравнения: sin 2 x + 7 cos 2 x + 7 = 0. Воспользуемся формулами, позволяющими выразить sin 2 x и cos 2 x через tg x . Получим

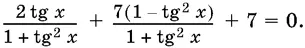
Приведя к общему знаменателю и отбросив знаменатель, который всегда отличен от нуля, получим простое уравнение

tg x = −7,

откуда x = −arctg 7 + π k , где k — любое целое число.

Хотя все произведенные преобразования кажутся «законными», мы легко убедимся в том, что целая серия корней x = π/ 2+ k π потеряна. Достаточно подставить эти значения неизвестного в исходное уравнение.

Корни были потеряны в результате применения неабсолютных тождеств

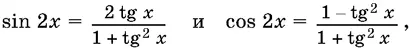
левые части которых существуют всегда, а правые теряют смысл

именно при x = π/ 2+ k π.

Если по каким-то причинам мы не могли избежать применения неабсолютных тождеств, грозящих потерей корней, то нам не остается ничего иного, как проверить те значения неизвестного, которые оказались исключенными из области определения входящих в уравнение выражений. В нашем примере, как и в большинстве тригонометрических уравнений, это нетрудно сделать.

Наконец, отметим такой важный момент при решении уравнений, как правильное использование условий.

Уравнение

lg (1 + x ) + 3 lg (1 − x ) = lg (1 − x ²) − 2

удобнее всего решать, преобразовав lg (1 − x ²) в сумму логарифмов. Чтобы оградить себя от возможной потери корней, мы должны написать

lg (1 − x ²) = lg |1 + x | + lg |1 − x |.

Однако подобная осторожность в этом примере является излишней. Поскольку в уравнение наряду с выражением lg (1 − x ²) входят lg (1 + x ) и lg (1 − x ), то 1 + x и 1 − x должны быть положительными, чтобы левая часть уравнения имела смысл. Поэтому вместо lg |1 + x | и lg |1 − x | можно написать lg (1 + x ) и lg (1 − x ). Таким образом, данное уравнение принимает вид

lg (1 + x ) + 3 lg (1 − x ) = lg (1 + x ) + lg (1 − x ) − 2.

Приведя подобные члены, получим

2 lg (1 − x ) = −2,

откуда x = 0,9 — единственный корень данного уравнения.

На этом примере мы видим, что правильное использование условия позволяет быстрее достичь цели, чем в случае чисто формальных преобразований.

Однако достаточно ли обоснованным было приведенное выше решение? Чтобы убедиться в этом, решите самостоятельно такое уравнение

lg (1 + x ) + 3 lg (1 − x ) = lg (1 − x ²) + 2.

Оно отличается от предыдущего лишь знаком последнего члена. Поэтому, повторив все приведенные только что рассуждения, получим

2 lg (1 − x )= 2,

откуда x = −9. Подставив это значение x в исходное уравнение, убеждаемся в том, что нами найден посторонний корень. Произошло это потому, что уравнения

lg (1 + x ) + 3 lg (1 − x ) = lg (1 + x ) + lg (1 − x ) + 2

и

2 lg (1 − x ) = 2

неравносильны. Равносильность нарушилась в результате уничтожения в правой и левой частях уравнения члена lg (1 + x ), который существенно ограничивал область определения уравнения. Таким образом, проверка здесь является необходимой частью решения.

Разобранный пример нередко предлагают решать так. Найдем область определения уравнения:

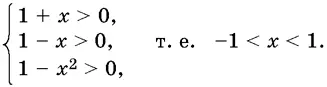
Теперь будем применять к уравнению те преобразования, которые не могут привести к потере корней:

lg (1 + x) + lg (1 − x)³ = lg (1 − x²) + lg 100,

lg [(1 + x)(1 − x)³] = lg 100(1 − x²),

(1 + x)(1 − x)³ = 100(1 − x²).

Решая последнее уравнение, найдем х 1= 1, х 2= −1, х 3= −9, х 4= 11. Так как все четыре числа не попали в интервал −1 < x < 1, то исходное уравнение не имеет корней.

Для данного уравнения такой метод решения оказывается верным, так как позволяет отбросить все найденные значения x. Однако основан он на ошибочном убеждении, что в процессе преобразований могут быть приобретены лишь те посторонние корни, которые не попадают в область определения исходного уравнения.

Приведем два примера.

Вначале рассмотрим уравнение

arcsin x = π/ 3+ arcsin x / 2.

Его область определения — отрезок −1 ≤ x ≤ 1. Возьмем синусы от правой и левой частей уравнения, в результате чего получим следствие

sin (arcsin x ) = sin ( π/ 3+ arcsin x / 2), т. е.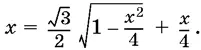

Решая последнее уравнение, получим х 1= −1, х 2= 1. Оба значения x принадлежат области определения исходного уравнения, однако х 2= −1 — посторонний корень, в чем легко убедиться проверкой.

Решим теперь в области действительных чисел уравнение

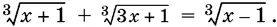
Областью определения этого уравнения является вся числовая ось. Возведем данное уравнение в куб:

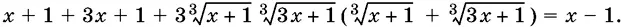
В последнее уравнение входит выражение 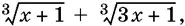являющееся левой частью данного уравнения. Заменяем его правой частью этого уравнения. Получим

Возведя в куб, получим

( x + 1)(3 x + 1)( x − 1) = −( x + 1)³,

откуда x 1= −1, x 2= 0.

Проверка убеждает нас в том, что корень x 2= 0 является посторонним. Он появился в результате замены левой части данного уравнения на не равную ей тождественно правую часть.

Приведенные примеры свидетельствуют о том, что нахождение области определения уравнения (или, как иногда говорят, области допустимых значений — ОДЗ) не гарантирует нас от появления посторонних корней, т. е. не избавляет от необходимости делать проверку полученных в результате решения корней.

Это не означает, что находить область определения всегда бессмысленно. Можно привести много примеров, когда знание области определения существенно упрощает решение.