Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
9.10.Найдите действительные решения уравнения
| x ² − 3 · x / 2 − 1| = − x ² − 4 x + β
и определите, при каких значениях β оно имеет единственное [6] Два совпадающих решения считаются за одно.
действительное решение.
9.11.Решите систему
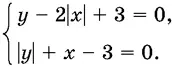
9.12.Найдите все действительные значения k , при которых решение системы
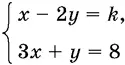
удовлетворяет условию: x > 1/ k , у > 0.
9.13.В области действительных чисел решите систему
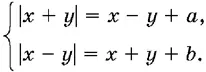
9.14.При каких значениях а система
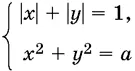
имеет действительные решения? Найдите эти решения.
Решите системы:
9.15.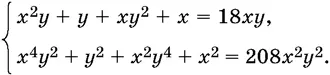 
9.16.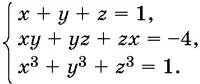 
9.17.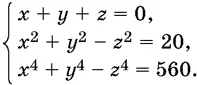 
9.18. 
9.19.Числа x , у и z удовлетворяют системе уравнений
где а, b, с не равны друг другу. Найдите x ³ + у ³ + z ³.
Решите системы:
9.20.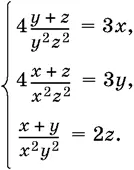 
9.21.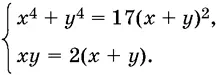 
9.22.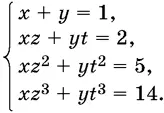 
9.23.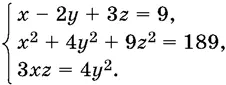 
9.24.Найдите все действительные решения системы
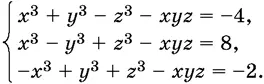
9.25.Найдите одно решение системы
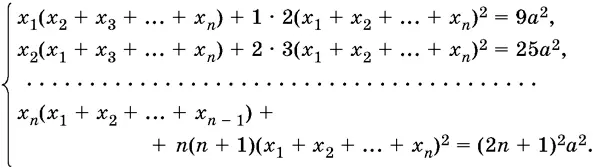
Решите системы в области действительных чисел:
9.26.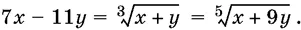 
9.27.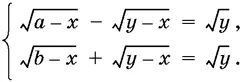 
9.28.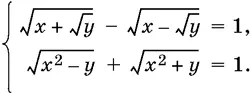 
9.29.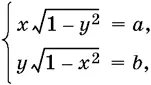 
если а > b > 0 и а + b < 1.
9.30.Найдите все значения а и b , при которых система
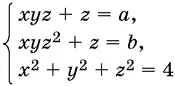
имеет единственное решение ( а , b , x , у — действительные числа).
9.31.Найдите все значения а , при которых система
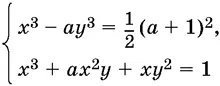
имеет хотя бы одно решение и всякое ее решение удовлетворяет уравнению x + у = 0 ( а , x , у — действительные числа).
9.32.Найдите все значения а , при которых система
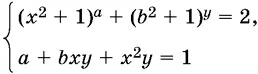
имеет хотя бы одно решение для любого значения b ( а , b , x , у — действительные числа).
9.33.Найдите все значения а и b , при которых система уравнений
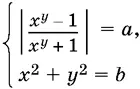
имеет единственное решение ( x , у , а , b — действительные числа, x > 0).
9.34.Решите систему
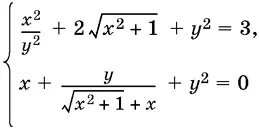
в области действительных чисел.
9.35.Решите уравнение
|6 − | x − 3| − | x + 1|| − аx − 5 а = 4
при всех действительных значениях параметра а .
9.36.При всех действительных а решите уравнение
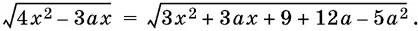
9.37.Решите уравнение
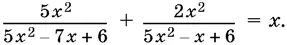
9.38.Решите систему уравнений
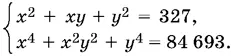
Глава 10
Алгебраические неравенства
О доказательстве неравенств.Доказать неравенство можно следующими способами, которые мы продемонстрируем на примере неравенства
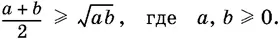
1. От противного. Предположим противное:
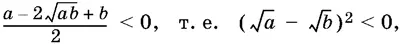
Тогда
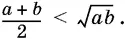
что невозможно.
2. По определению неравенства. Составим разность левой и правой частей и определим ее знак:
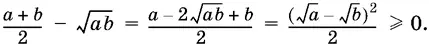
3. Вывести из ранее доказанного или очевидного неравенства. Мы знаем, что
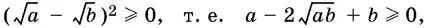
откуда
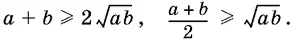
Обратите внимание, что следующее «доказательство» неравенства является логически некорректным.
Если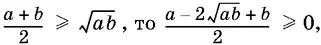 
и, следовательно,
Интервал:
Закладка:
