Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
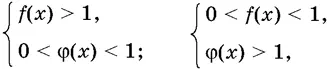
или системе неравенств
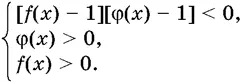
Решения неравенств f ( x ) φ( x )< 1 и f ( x ) φ( x )> 1 в предположении, что допускаются отрицательные значения f ( x ), разобраны в задачах 10.29, 10.30, 10.32.
Запомнить эти свойства можно следующим образом: степень больше единицы, если основание и показатель степени одинаково расположены по отношению к единице и нулю соответственно (т. е. основание правее единицы и показатель правее нуля или основание левее единицы и показатель левее нуля); логарифм больше нуля, если основание и логарифмируемое выражение одинаково расположены по отношению к единице. Если расположение элементов, о которых шла речь, неодинаково, то степень меньше единицы, а логарифм меньше нуля.
10.1.Докажите, что если а + b = 2, где а и b — действительные числа, то а 4+ b 4 ≥ 2.
10.2.Докажите, что
(1 + a 1)(1 + а 2)...(1 + а n ) ≥ 2 n ,
если а 1, а 2, ..., а n , а n — положительные числа и а 1 а 2... а n = 1.
10.3.Дано а + b = с , где а , b , с — положительные числа. Докажите, что
а ⅔+ b ⅔> с ⅔.
10.4.Докажите, что − x ³ + x ² ≤ ¼, если 0 ≤ x ≤ 1.
10.5.Докажите неравенство
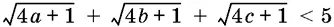
при условии, что а + b + с = 1, а подкоренные выражения неотрицательны.
10.6.Докажите неравенство
( а + b ) n < 2 n ( а n + b n ),
если а > 0, b > 0, n — натуральное число.
10.7.Докажите, что при а > b > 0 и p > q где а , b и с — положительные и не равные друг другу числа, не пользуясь неравенствами между средним арифметическим и средним геометрическим трех чисел.
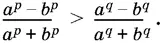
10.8.Докажите, что 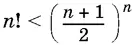 при n > 1.
при n > 1.
10.9.Докажите неравенство
a / b + b / c + c / a > 3
где а , b и с — положительные и не равные друг другу числа, не пользуясь неравенствами между средним арифметическим и средним геометрическим трех чисел.
10.10.Докажите, что
а ² + b ² + с ² ≥ 4 S √3,
где а , b , с — стороны, а S — площадь некоторого треугольника.
10.11.Докажите, что
( x − 1)( x − 3)( x − 4)( x − 6) + 10 ≥ 1
при всех действительных значениях x .
10.12.Докажите, что если действительные числа x , у , z , не равные нулю, удовлетворяют равенствам:
x + у + z = xуz и x ² = уz ,
то
x ² ≥ 3.
10.13.Докажите, что если x , у , z — действительные числа, удовлетворяющие равенствам
x + у + z = 5, уz + z x + x у = 8,
то
1 ≤ x ≤ 7/ 3, 1 ≤ y ≤ 7/ 3, 1 ≤ x ≤ 7/ 3. [9] Так в источнике (прим. от верстальщика fb2).
10.14. Решите неравенство
аx ² + x + 1 > 0,
где а ≠ 0 — произвольное действительное число.
10.15. Найдите все действительные значения m , при которых квадратный трехчлен x ² + mx + ( m ² + 6 m ) будет отрицателен при всех значениях x , удовлетворяющих неравенству 1 < x < 2.
10.16. Найдите все действительные значения а , при которых корни многочлена x ² + x + а будут действительными и оба корня будут больше а .
10.17.При каких значениях к корни многочлена
k ² x ² + kx − 2
будут действительными и один корень по абсолютной величине будет больше 1, а другой по абсолютной величине будет меньше 1?
10.18.Найдите все действительные значения m , для которых неравенство
тx ² − 4 x + 3 m + 1 > 0
удовлетворяется при всех положительных значениях x .
Решите неравенства:
10.19.| x ² − 2 x − 3| < 3 x − 3.
10.20.| x − 3| > | x + 2|.
10.21. 
10.22. 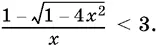
10.23. 
10.24. 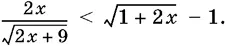
10.25. 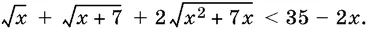
10.26. 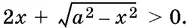
10.27.4 x ≤ 3 · 2 √ x + x + 4 √ x +1.
10.28.4 x ² + 3 √ x +1+ x · 3 √ x < 2 x ² · 3 √ x + 2 x + 6.
10.29 [10] Требуется найти не только положительные значения x .
. 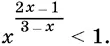
Решите неравенства:
10.30.(4 x ² + 12 x + 10) | x ³ − 5 x + 2| ≥ (4 x ² + 12 x + 10) x − 2.
10.31. x log аx +1> а ² x .
10.32 [11] Требуется найти не только положительные значения x .
. 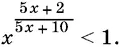
10.33. 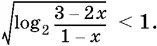
10.34. 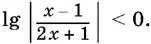
10.35. 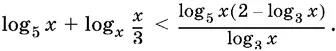
10.36.log 2(2 x − 1) log ½(2 x + 1− 2) > −2.
10.37.log | x + 6|2 · log 2( x ² − x − 2) ≥ 1.
10.38. 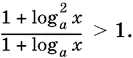
10.39.log kxx + log x ( kx ²) > 0, где 0 < k < 1.
10.40.log x [log 2(4 x − 6)] ≤ 1.
10.41. 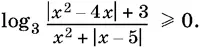
10.42. 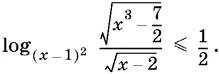
Интервал:
Закладка:










