Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы

3.36.Вначале нужно извлечь информацию из того обстоятельства, что проекции каждой стороны четырехугольника на взаимно перпендикулярные плоскости равны. Отсюда следует, что каждая сторона четырехугольника параллельна плоскости, делящей угол между взаимно перпендикулярными плоскостями пополам.

3.37.Задачу можно свести к такой: доказать, что объем конуса меньше куба его образующей. (!)

3.38.Введите линейные элементы, характеризующие конус, например высоту H и радиус основания ρ. Затем величины H , ρ и p выразите через радиусы R и r шаров.

3.39.Чтобы использовать данное в условии отношение объемов двух конусов, нужно выразить радиус основания одного конуса через радиус основания другого. Для этого придется внутренний конус, свободно вращающийся в шаре, закрепить так, чтобы образующие конусов были параллельны.

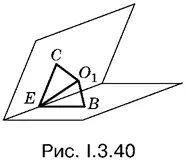
3.40.Не следует начинать решение с построения общего чертежа, который окажется весьма громоздким. Удобнее вначале провести анализ условия и вспомнить, что центр сферы, вписанной в двугранный угол (рис. I.3.40), лежит в плоскости, проходящей через точки касания В и С и перпендикулярной к ребру этого угла. Линейный угол ВЕС делится прямой EO 1пополам, а отрезки СЕ и ВЕ равны. Если сделать соответствующие построения для треугольной пирамиды, то появится возможность использовать условие, что данная пирамида правильная.

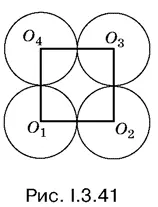
3.41.Центры четырех шаров, касающихся основания конуса, лежат в одной плоскости (рис. I.3.41). Если мы проведем осевое сечение конуса через O 1и О 3, то сможем связать высоту H и радиус основания R конуса с радиусом r .

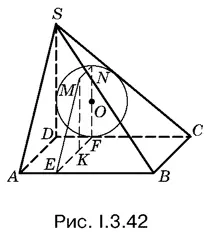
3.42.Необходимые построения показаны на рис. I.3.42. Плоскость EMNF проходит через ось цилиндра и перпендикулярна к основанию пирамиды; F — точка касания окружности основания цилиндра со стороной DС ; M — точка касания с гранью ASB . Отрезки МК и EF взаимно перпендикулярны, KF — искомая величина.

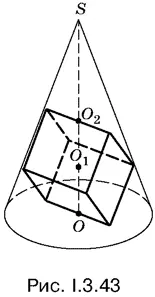
3.43.Условия задачи отражены на рис. I.3.43. Ввести линейные элементы, определяющие конус, и выразить их через ребро куба.

3.44.Поскольку в усеченную пирамиду вписан шар, то объем пирамиды можно представить в виде произведения одной трети радиуса шара на полную поверхность пирамиды. Обозначим стороны нижнего и верхнего основания через а и b соответственно. Воспользовавшись сравнением объемов, — в качестве второго выражения для объема нужно взять обычную формулу 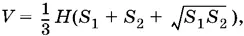— выразим площадь боковой грани пирамиды через а и b .

3.45.Нет необходимости изображать сами шары. Достаточно изобразить их центры и точки их касания с плоскостью.

3.46.Фигуры, о которых говорится в условии задачи, расположены так, что у них имеются две плоскости симметрии. Первая плоскость симметрии пройдет через ребро данного двугранного угла и через центр меньшего шара. На этой плоскости окажутся центры двух других шаров. Вторая плоскость симметрии будет перпендикулярна к ребру двугранного угла и тоже пройдет через центр меньшего шара. Поэтому достаточно сделать каркасный чертеж, на котором изобразить лишь одну из четырех равных частей данной конфигурации.

3.47.У рассматриваемой фигуры будут три плоскости симметрии, проходящие через ось конуса и центр одного из шаров. Проекции центров трех шаров на плоскость P образуют равносторонний треугольник, сторона которого равна 2 R . Сделать каркасный чертеж.

3.48.Чтобы использовать условие задачи, нужно рассмотреть два соседних конуса. При этом нет необходимости рисовать их целиком, достаточно изобразить оси, общую образующую и образующие, по которым конусы касаются плоскости.

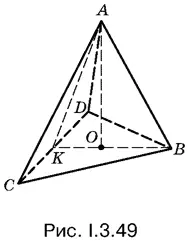
3.49.По условию сфера, радиус которой нужно найти, вписана в трехгранный угол А (рис. I.3.49). Это означает, что ее центр лежит на высоте АО . Однако все точки высоты АО (кроме концов) лежат внутри сферы, построенной на AB . Следовательно, касание двух сфер может быть только внутренним.

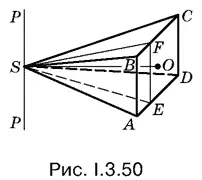
3.50.Искомое тело можно представить себе как часть пространства, заполненную в результате вращения вокруг оси РР (рис. I.3.50) треугольника SАВ и всех сечений пирамиды, проходящих через вершину S параллельно AB . Таким сечением является, например, треугольник SEF , изображенный на рис. I.3.50.

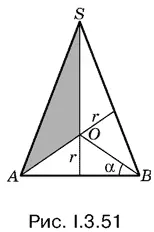
3.51. Способ 1.Задачу можно решить аналитически, если выразить полную поверхность конуса через радиус вписанного в него шара и угол а (рис. I.3.51; на нем изображено осевое сечение конуса). Затем следует воспользоваться соотношением S пк= 2 S ш. В результате получим тригонометрическое уравнение относительно α.

Способ 2.Объем конуса можно представить себе как сумму объемов V 1и V 2 где V 1— объем тела, полученного вращением треугольника ASO вокруг оси конуса, а V 2— объем конуса с осевым сечением АОВ .

3.52.Пусть АВС и А 1 В 1 С 1— основания призмы, а В 1 В — ее ребро, принадлежащее двум равновеликим граням. Докажите, что вершина В 1проецируется тогда на биссектрису одного из углов, образованных прямыми AB и BC . Может ли проекция вершины В 1оказаться на биссектрисе внешнего угла треугольника АВС ?

3.53.О пирамидах не сказано, какие они. Поэтому следует попытаться заполнить ими весь объем куба.

3.54.Высота SP пирамиды SABС (рис. I.3.54) фиксирована и равна 4. В основании правильный треугольник АВС со стороной 6. Кроме того, основание высоты не покидает треугольник АВС . Следовательно, вершина S пирамиды SАВС лежит в плоскости, параллельной плоскости треугольника АВС , и отстоящей от нее на расстоянии, равном 4. Если мы построим на основании АВС прямую призму А 1 В 1 С 1 ABC с ребром 4, то вершина S пирамиды SАВС будет принадлежать верхнему основанию этой призмы.