Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы
- Название:Сборник задач по математике с решениями для поступающих в вузы
- Автор:
- Жанр:
- Издательство:«ОНИКС 21 век» «Мир и Образование»
- Год:2003
- Город:Москва
- ISBN:5-329-00766-6, 5-94666-080-2
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Альберт Рывкин - Сборник задач по математике с решениями для поступающих в вузы краткое содержание
Основу задачника составили варианты письменных работ по математике, предлагавшихся на вступительных экзаменах в ряде ведущих вузов Москвы.
Сборник содержит около 500 типовых задач. K каждой задаче дается до трех указаний, помогающих найти правильный путь к решению, а затем приводится подробное решение.
Пособие может использоваться при самостоятельной подготовке к экзаменам в вуз, а также на подготовительных отделениях и курсах.
Сборник задач по математике с решениями для поступающих в вузы - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
9.7.Поскольку неизвестное входит в уравнение либо в сочетании x − b , либо в сочетании а − x , то удобно ввести обозначения 
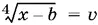 и получить систему алгебраических уравнений.
и получить систему алгебраических уравнений.
9.8.Ввести вспомогательное неизвестное у и свести решение данного уравнения к решению системы уравнений относительно x и у .
9.9.Перенести 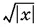 в правую часть уравнения и возвести обе части в квадрат.
в правую часть уравнения и возвести обе части в квадрат.
9.10.Чтобы избавиться от знаков абсолютной величины, можно поступить двояко: либо потребовать, чтобы правая часть уравнения была неотрицательной, и решить уравнения
x ² − 3 x / 2− 1 = − x ² − 4 x + β, x ² − 3 x / 2− 1 = x ² + 4 x − β;
либо рассмотреть два случая: в первом выражение, стоящее под знаком абсолютной величины, неотрицательно, а во втором — отрицательно.
9.11.Рассмотреть различные случаи расположения x и у по отношению к нулю (всего придется рассмотреть четыре случая). (!)
9.12.Решить систему уравнений с параметром k , а затем решить систему неравенств. (!)
9.13.Рассмотреть различные случаи взаимного расположения чисел x и у и чисел x и − у . Это позволит раскрыть знаки абсолютной величины. (!)
9.14.Второе уравнение — уравнение окружности радиуса √ а . Нарисовать кривую, которая определяется первым уравнением.
9.15.Одно решение очевидно: x = у = 0. Если ху ≠ 0, то можно разделить первое уравнение на ху, а второе на x ² у ².
9.16.Если бы во втором и третьем уравнениях не было коэффициентов 2 и 3, то уравнения системы получались бы друг из друга с помощью циклической перестановки неизвестных x , у и z . Однако влияние коэффициентов оказывается столь сильным, что попытка использовать это свойство системы не приводит к успеху. Попытайтесь преобразовать систему в распадающуюся, для чего потребуется отыскать алгебраическое выражение, общее для двух уравнений, и исключить его.
9.17.Если первое уравнение системы записать в виде x + у = − z и возвести в квадрат, то с помощью второго ее уравнения можно найти ху .
9.18.Сопоставьте первое и последнее уравнения. Если записать их в виде
x + у = 1 − z , х ³ + у ³ = 1 − z ³,
то напрашивается способ, с помощью которого можно преобразовать систему в распадающуюся.
9.19.Если раскрыть скобки, то получим систему линейных уравнений относительно u = x + у + z , v = ху + xz + yz , w = xyz. Найдя u , v и w , можно вычислить х ³ + у ³ + z ³, если возвести x + у + z = u в куб: u ³ = х ³ + у ³ + z ³ + 3 uv − 3 w .
Однако такой путь решения, хотя и прост по идее, требует значительных выкладок. Решение можно упростить, если ввести в рассмотрение многочлен M ( t ) = ( t − x )( t − у )( t − z ) + а, который в силу условия задачи имеет корни t = а, t = b , t = с .
9.20.Первые два уравнения системы симметричны относительно x и у . Нужно использовать эту симметрию для того, чтобы получить одинаковые правые части у этих двух уравнений.
9.21.Если второе уравнение возвести в квадрат, то можно сравнить два выражения для ( x + у )². (!)
9.22.В первое уравнение входит у , в последующие уt , yt ² и yt ³ соответственно. Эта закономерность позволяет исключить у .
9.23.Каждый элемент, стоящий в левой части второго уравнения, получается из соответствующего элемента, стоящего в левой части первого уравнения, возведением в квадрат. Нужно использовать это свойство системы.
9.24.Левые части всех трех уравнений симметричны относительно x , у , z . Поэтому, подвергнув какому-то преобразованию любые два уравнения системы, разумно сделать то же самое и с оставшимися двумя парами уравнений.
9.25.Если известна сумма s = x 1+ x 2+ ... + x n , то из каждого уравнения можно найти соответствующее x k .
9.26.Чтобы избежать возведения двучлена в третью и, тем более, в пятую степень, нужно ввести новые неизвестные так, чтобы выражение 7 x − 11 у было одним из этих неизвестных.
9.27.Поскольку 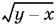 входит в оба уравнения с разными знаками, а √ у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.
входит в оба уравнения с разными знаками, а √ у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.
9.28.Чтобы левые части уравнений стали однородными относительно неизвестных, удобно ввести новое неизвестное z = √ у .
9.29.Если каждое из уравнений возвести в квадрат, то получим систему относительно u = x ² и v = у ². Проверка здесь может оказаться довольно сложной, поэтому целесообразно следить за равносильностью в процессе решения. Чтобы в результате возведения в квадрат не появились посторонние решения, достаточно записать ограничения: x > 0, у > 0.
9.30.Все члены системы, содержащие x и у , однородны второй степени относительно x и у . Пусть данная система имеет решения x 1, у 1, z 1Укажите симметричное решение, которое наряду с этим будет иметь система.
9.31.Поскольку вместе с условием x + у = 0 мы получаем три уравнения с двумя неизвестными, то имеет смысл воспользоваться подстановкой у = − x .
9.32.Поскольку данная система должна иметь решение при любом b , то, чтобы сузить область допустимых значений а , можно рассмотреть эту систему при некотором фиксированном b .
9.33.Вначале нужно использовать условие, что система должна иметь только одно решение. Второе уравнение можно рассматривать как четную функцию относительно x и у , т. е. наряду с решением x = x 1, у = у 1оно имеет три симметричных решения: (− x 1, у 1), ( x 1, − у 1), (− x 1, −у 1). Какое из этих решений наряду с ( x 1, у 1) будет удовлетворять первому уравнению?
9.34.Второе уравнение можно преобразовать к виду
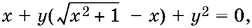
умножив числитель и знаменатель дроби на выражение, сопряженное знаменателю. Легко убедиться, что у ≠ 0. Поэтому можно полученное уравнение разделить на у , после чего нетрудно с помощью первого уравнения системы исключить 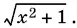
Интервал:
Закладка:










