Генри Дьюдени - Кентерберийские головоломки

164. Четыре кенгуру.Сначала я хочу пояснить, что рисунок изображает 64 загона, отделенных друг от друга изгородями, которые находятся где-то в Австралии. Я, конечно, далек от того, чтобы утверждать, будто наши родичи «с той половины» всегда разгораживают свои земли столь методичным образом. Можно заметить, что на каждом угловом участке сидит по кенгуру. Я не могу вам объяснить, почему кенгуру имеют пристрастие именно к угловым участкам, но по поводу того, что они всегда прыгают ходом коня, с уверенностью берусь утверждать, что «ход коня» был бы непременно «ходом кенгуру», если бы шахматы не были изобретены задолго до кенгуру.

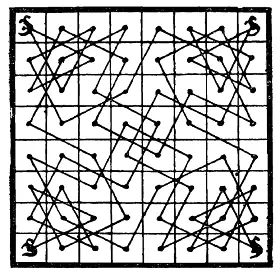
Так вот головоломка состоит в следующем. Однажды утром каждый кенгуру отправился на прогулку и, сделав 16 последовательных ходов коня, посетил ровно 15 различных загонов и вернулся в свой угол. Н-и один загон не посещался более чем одним кенгуру. На рисунке показано, как им удалось это сделать. Вам же нужно показать, каким образом они могли бы добиться своей цели, чтобы при этом ни один кенгуру не пересек центральной горизонтальной прямой, разбивающей квадрат на две равные части.

165. Доска, разбитая на отсеки.Нельзя разбить обычную шахматную доску на 4 равных квадратных отсека и описать конем полное турне или даже только путь в каждом из них. Однако, разделив доску на 4 части, как это показано на рисунке (две части по 12 клеток, а две другие – по 20), можно получить интересную головоломку. Вам предлагается проделать полное турне на этой доске, начав с любой клетки, но переходя из одного отсека в другой не прежде, чем посетив все клетки данного отсека и сделав последний ход конем в исходную клетку. Это сделать нетрудно, но головоломка окажется весьма занимательной и небесполезной.

Возможно ли «турне» или полный «путь» коня на прямоугольной доске заданных размеров, зависит не только от размеров доски, но и от ее формы. Турне, очевидно, невозможно на доске, содержащей нечетное число ячеек, такой, как 5×5 или 7X7, и вот почему. Каждый последовательный скачок коня должен совершаться с белой клетки на черную и с черной на белую поочередно. Но если число клеток, или ячеек, нечетно, то число клеток одного цвета на 1 больше числа клеток другого цвета. Следовательно, путь должен начинаться с клетки того цвета, которого больше, и заканчиваться тем же цветом, а поскольку ход конем между клетками одинакового цвета невозможен, то путь не может быть возвратным. Однако правильное турне можно совершить на прямоугольной доске любых размеров, содержащей четное число клеток, если число клеток на одной ее стороне не меньше 6, а на другой – не меньше 5. Другими словами, наименьшей прямоугольной доской, на которой возможно турне, будет доска 6×5.

Полный путь коня (не возвратный) по всем клеткам доски невозможен на доске, у которой размер одной из сторон равен всего лишь 2 клеткам, а также на квадратной доске меньше 5×5. Так что на доске 4×4 мы не сможем совершить конем ни турне, ни даже полного пути; одну клетку придется оставить непосещенной. И все же на доске 4×3, содержащей на 4 клетки меньше, полный путь удается совершить 16 различными способами. Читатель, быть может, захочет отыскать их сам. Каждый путь, начинающийся или заканчивающийся на других клетках, здесь считается другим решением, так же как и путь, получающийся с помощью поворота.

166. Турне четырех коней.Я повторяю, что если разбить шахматную доску на 4 равные части, как показано на рисунке жирными линиями, то на одной из частей невозможно осуществить турне коня.

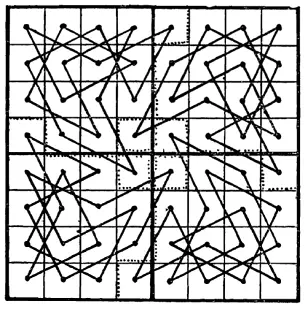
На рисунке вы видите лучшую из попыток такого турне, при которой конь дважды вынужден выйти за пределы своего участка. Попробуйте разбить доску на 4 части одинаковых размеров и формы так, чтобы на каждой из них оказалось возможным осуществить турне коня. Разрезы вдоль пунктирных линий не подходят, ибо тогда 4 центральные клетки оказались бы отделены либо просто висели бы на ниточке.

167. Кубическое турне коня.Несколько лет назад я где-то прочитал, что Абни Вандермонд, известный математик, который родился в 1736 г., а умер в 1793 г., большое внимание уделял турне коня. Я не уверен относительно точных результатов его исследований, но один момент привлек мое внимание: он поставил вопрос о турне коня на шести гранях куба, каждая из которых представляет собой шахматную доску. Нашел ли он решение или нет, я не знаю, но я нигде не встречал опубликованного решения, а поэтому сразу же сел за изучение этой интересной задачи. Может быть, читатель захочет ею заняться?

168. Четыре лягушки.На рисунке показано восемь грибков, на 1-м и 3-м из них сидят белые лягушки, а на 6-м и 8-м – черные.

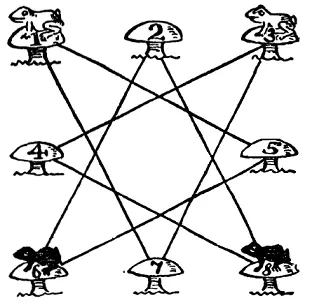
Головоломка состоит в том, чтобы, передвигая за один раз по одной лягушке в любом порядке вдоль прямых линий от одного грибка до другого, поменять лягушек местами, то есть черные лягушки должны занять грибки 1 и 3 , а белые – 6 и 8. Воспользовавшись четырьмя шашками и приведенной схемой, вы найдете эту задачу совсем простой, но несколько труднее будет сделать это за 7 перемещений, где любое число последовательных ходов одной лягушки считается одним перемещением. Разумеется, на одном грибке одновременно может сидеть лишь одна лягушка.

169. Головоломка мандарина.Следующая головоломка обладает особой пикантностью, так как ее правильное решение позволило одному молодому китайцу добиться руки своей возлюбленной. Хи-Чум-Чоп был богатейшим мандарином во всей округе на сотню миль от Пекина, не счесть было числа поклонников его прекрасной дочери Пики-Бо. Самым пылким из них оказался Винки-Хи. Когда он попросил у старого мандарина руки его дочери, тот предложил ему головоломку, пообещав свое согласие, если юноша принесет ему правильный ответ в течение недели. Винки-Хи, следуя обычаю, принятому среди некоторых любителей головоломок и до сего дня, предложил головоломку всем своим друзьям, а затем, сравнив решения, лучшее выдал за собственное. Мандарин выполнил свое обещание. Для свадебного пира был заколот откормленный щенок, и когда Хи-Чум-Чоп передал Винки-Хи, согласно китайскому обычаю, кусок печенки, то гости расценили это как пожелание вечного благополучия.