Стивен Строгац - Удовольствие от Х.Увлекательная экскурсия в мир математики от одного из лучших преподавателей в мир

С помощью нижеприведенной аналогии я надеюсь пролить свет на основную идею фундаментальной теоремы и то, зачем она нужна. (Ее предложил мой коллега Чарли Пескин из Нью-Йоркского университета.) Представьте себе лестницу, общее изменение высоты которой от нижней до верхней ступенек равно сумме высот всех ступенек. Это верно даже при условии, что высота одних ступенек больше, чем других. Количество ступенек не имеет значения.

Фундаментальная теорема интегрального исчисления работает и для функций. Если проинтегрировать производную функции от одной точки до другой, то получим ее изменение между двумя точками. В данной аналогии функции — это увеличение подъема каждой ступеньки по отношению к уровню земли. Высоты отдельных ступенек — производные. Интегрирование производных — это суммирование подъемов. А две точки — верхняя и нижняя часть лестницы.

Что это нам дает? Предположим, вас попросили просуммировать огромный список чисел. Оказывается, что бы вы ни суммировали, всякий раз вы берете интеграл по частям. Если вам удастся найти соответствующие лестницы — другими словами, если вы сможете отыскать функцию подъема, для которой подходят эти числа, — то вычислить интеграл совсем несложно. Просто нужно из верха вычесть низ [95] По сути, в этой аналогии говорится о том, что если вы можете найти первообразную для подынтегральной функции, то определенный интеграл от нее равен разности первообразной в точках — пределах интегрирования. Прим. ред. .

Это огромное достижение в ускорении вычисления стало возможным благодаря фундаментальной теореме интегрального исчисления. Именно поэтому с первых месяцев преподавания курса интегрального исчисления мы требуем от студентов нахождения функции возвышения, что в математике называется первообразной или неопределенным интегралом.

С точки зрения перспективы надежным наследием интегрального исчисления будет своего рода взгляд Veg-O-Matic [96] См. примечание переводчика о заголовке главы. Прим. ред. Хоть ломтиками, хоть кубиками (It Slices, It Dices) — это выражение было слоганом рекламной кампании на телевидении одного из первых (если не первого) кухонных комбайнов торговой марки Veg-O-Matic, выпущенного в 1961 году. Комбайн мог измельчать продукты в виде ломтиков и кубиков. Позже это выражение вошло в обиход в значении «быть многофункциональным». Прим. перев. на Вселенную. Ньютон и его преемники обнаружили, что сама природа открывается по кусочкам. Оказалось, что таким свойством обладают практически все открытые за последние 300 лет законы физики, что бы они ни описывали: движение частиц, тепловые потоки, электричество, воздух или воду. Вместе с основополагающими законами условия в каждом кусочке времени или пространства определят, что произойдет в соседних кусочках. Впервые в истории рациональное прогнозирование стало возможным — не в час по чайной ложке, а семимильными шагами благодаря фундаментальной теореме.

Так что давно пора поменять наш лозунг для интегралов «Хоть ломтиками, хоть кубиками» на «Пересчитайте заново. Есть метод получше».

Некоторые числа — такие знаменитости, что их эстрадные имена состоят всего лишь из одной буквы. Даже самые важные персоны, такие как Мадонна и Принц, не могут с ними сравниться. Самое знаменитое — число π, ранее известное как 3,14159…

Следом идет число i из алгебры — это мнимое число настолько радикально, что изменило само понятие числа. Кто там далее в «звездном» рейтинге?

Поприветствуйте e ! Прозванное так за свою роль в прорыве экспоненциального роста, число e теперь Зелиг [97] «Зелиг» — кинофильм режиссера Вуди Аллена (1983), действие которого происходит в Америке 1920–1930-х годов. В фильме рассказывается о необычном еврее по фамилии Зелиг, умеющем перевоплощаться в людей, с которыми он общается. Прим. перев. высшей математики. Оно всплывает везде, где можно и нельзя, выглядывает из углов сцены, дразня своим присутствием в нелепых местах. Например, наряду с глубоким математическим анализом, оно вызывает цепную реакцию и бум рождаемости населения; е есть что сказать о том, со сколькими партнерами вы должны иметь романтические отношения прежде, чем остепенитесь.

Но перед тем как перейти к этим вопросам, давайте точно определим, что означает число e [98] Все ипостаси числа e и экспоненциальной функции представлены в книге E. Maor, e: The Story of a Number (Princeton University Press, 1994). Читатели, которые знакомы с интегральным исчислением, насладятся статьей B. J. McCartin, e: The master of all, Mathematical Intelligencer, Vol. 28, № 2 (2006), pp. 10–21. PDF-версия доступна по адресу http://mathdl.maa.org/images/upload_library/22/Chauvenet/mccartin.pdf. . Его численное значение равно 2,71828 — но это не многое разъясняет. Я могу вам сказать, что e равно пределу суммы

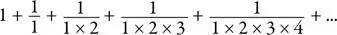
по мере увеличения числа членов, участвующих в этой сумме. Но это тоже не особенно полезно. Давайте лучше посмотрим на е в действии.

Представьте себе, что у вас есть депозит в виде сберегательного счета в размере 1000 долларов в банке, который ежегодно выплачивает невероятно щедрую процентную ставку в 100 % годовых. Через год на вашем счете будет 2000 долларов, то есть начальный депозит в размере 1000 долларов плюс 100-процентная ставка по ним, равная еще 1000 долларам.

Прикидываясь дурачком, вы просите у банка еще более выгодные условия: предлагаете выплачивать вам проценты раз в полгода, то есть чтобы банк выплачивал только 50 % ставки в течение первых шести месяцев и 50 % ставки следующие шесть месяцев. Естественно, вы окажетесь в выигрыше, так как будете получать проценты на проценты. Но насколько?

Ответ на этот вопрос следующий: ваша первоначальная сумма в 1000 долларов возрастет на коэффициент 1,50 за первое полугодие и снова на коэффициент 1,50 во втором полугодии. А поскольку 1,50, умноженное на 1,50, равно 2,25, то через год на вашем счете будет 2250 долларов. Это значительно больше, чем 2000 долларов, которые вы можете получить на изначальных условиях.

А что произойдет, если вы еще надавите на банк и убедите его разбить год на более короткие периоды выплаты процентов: по дням, секундам или даже по наносекундам? В этом случае вы смогли бы сколотить небольшое состояние?

Допустим, год поделен на 100 равных периодов, после каждого из которых выплачивается 1 % ставки (при процентной ставке 100 % в год, поделенной на 100 частей). Тогда в конце года сумма в 1000 долларов увеличится на коэффициент 1,01, возведенный в 100-ю степень, что приблизительно равно 2,70481. Другими словами, вместо 2000 или 2250 долларов на вашем счете будет б о льшая сумма, но не превышающая 2704,81 доллара.