Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

Рассмотрим плоскость, рассекающую небесную сферу перпендикулярно оси вращения, проходящей через центр Земли и небесной сферы. Эта плоскость пересечет земную поверхность вдоль большого круга — земного экватора, а также небесную сферу — вдоль ее большого круга, который называется небесным экватором. Второй аналогией с земными параллелями и меридианами будет небесный меридиан, проходящий через два полюса и расположенный в плоскости, перпендикулярной экватору. Так как все небесные меридианы, подобно земным, равны, нулевой меридиан можно выбрать произвольно. Выберем в качестве нулевого небесный меридиан, проходящий через точку, в которой находится Солнце в день весеннего равноденствия. Положение любой звезды и небесного тела определяется двумя углами: склонением и прямым восхождением, как показано на следующем рисунке. Склонение — это угол между экватором и звездой, отсчитываемый вдоль меридиана места (от 0 до 90° или от 0 до —90°). Прямое восхождение — это угол между точкой весеннего равноденствия и меридианом звезды, отсчитываемый вдоль небесного экватора. Иногда вместо прямого восхождения используется часовой угол, или угол, определяющий положение небесного тела относительно небесного меридиана точки, в которой находится наблюдатель.

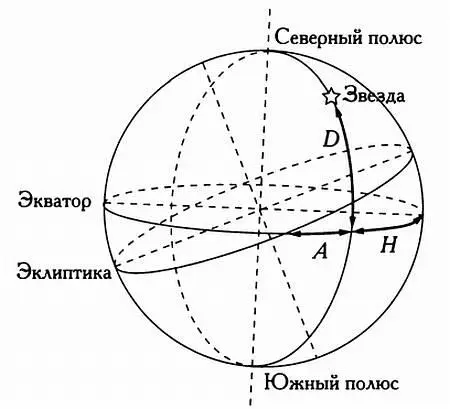
Положение звезды, заданное экваториальными ( A, D) и часовыми координатами ( Н, D).

Преимущество второй экваториальной системы координат (склонения и прямого восхождения) очевидно: эти координаты будут неизменными вне зависимости от положения наблюдателя. Кроме того, в них учитывается вращение Земли, что позволяет скорректировать вносимые им искажения. Как мы уже говорили, видимое вращение небесной сферы вызвано вращением Земли. Похожий эффект возникает, когда мы сидим в поезде и видим, как рядом с нами движется другой поезд: если не смотреть на перрон, то нельзя определить, какой из поездов на самом деле тронулся с места. Нужна точка отсчета. Но если вместо двух поездов рассматривать Землю и небесную сферу, найти дополнительную точку отсчета будет не так-то просто.

В 1851 году француз Жан Бернар Леон Фуко(1819–1868) провел эксперимент, демонстрирующий движение нашей планеты относительно небесной сферы.

Он подвесил груз весом 28 килограммов на проволоке длиной 67 метров под куполом парижского Пантеона. Колебания маятника Фуко продолжались 6 часов, период колебаний составил 16,5 секунды, отклонение маятника — 11° в час. Иными словами, с течением времени плоскость колебаний маятника смещалась относительно здания. Известно, что маятники всегда движутся в одной плоскости (чтобы убедиться в этом, достаточно подвесить на веревке связку ключей и проследить за ее колебаниями). Таким образом, наблюдаемое отклонение могло быть вызвано только одной причиной: само здание, а следовательно, и вся Земля, вращались вокруг плоскости колебаний маятника. Этот опыт стал первым объективным доказательством вращения Земли, и маятники Фуко были установлены во многих городах.

Портрет Жана Бернара Леона Фукои маятник в парижском Пантеоне.

Земля, которая кажется неподвижной, вращается не только вокруг своей оси, совершая полный оборот за 24 часа (что эквивалентно скорости примерно в 1600 км/ч, то есть 0,5 км/с, если мы находимся на экваторе), но и вокруг Солнца, совершая полный оборот за 365,2522 дня (со средней скоростью примерно 30 км/с, то есть 108000 км/ч). Более того, Солнце вращается относительно центра нашей галактики, совершая полный оборот за 200 млн лет и двигаясь со скоростью 250 км/с (900000 км/ч). Но и это еще не все: наша галактика удаляется от остальных. Таким образом, движение Земли больше похоже на головокружительную карусель в парке аттракционов: мы вращаемся вокруг себя, движемся в пространстве и описываем спираль с головокружительной скоростью. При этом нам кажется, что мы стоим на месте!

Хотя в астрономии используются и другие координаты, описанные нами системы наиболее популярны. Осталось ответить на последний вопрос: как перевести координаты из одной системы в другую? Заинтересованный читатель найдет описание всех необходимых преобразований в приложении.

* * *

МОДЕЛЬ ЭКСПЕРИМЕНТА ФУКО

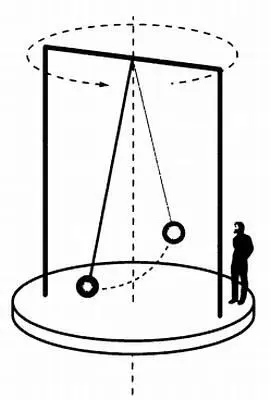
Предлагаем читателю провести простой эксперимент. Возьмем круглую коробку и приклеим на нее лист плотного картона или фанеры, на котором закрепим небольшую раму в форме футбольных ворот, как показано на рисунке. Поместим в угол листа куклу, которая будет играть роль наблюдателя. Привяжем к горизонтальной планке рамы нить, на которой закрепим грузило.

Отведем получившийся маятник в сторону и отпустим. Маятник будет колебаться параллельно одной из стен комнаты, в которой мы находимся. Если мы начнем плавно вращать лист фанеры вместе с круглой коробкой, то увидим, что рама и кукла начнут смещаться относительно стены комнаты, но плоскость колебаний маятника будет по-прежнему параллельна стене.

Если мы представим себя в роли куклы, то увидим, что маятник движется относительно пола, но при этом мы не сможем ощутить движение коробки и рамы, на которой он закреплен. Аналогично, когда мы наблюдаем за маятником в музее, то нам кажется, что плоскость его колебаний смещается, однако на самом деле смещаемся мы сами вместе со зданием музея и всей Землей.

* * *

Определить углы, указывающие положение любого астрономического объекта, сравнительно просто. По сути, эта система координат ничем не отличается от той, что используют игроки в морской бой. По-настоящему трудная задача, о которой мы упомянули в начале главы, заключается в определении расстояния до наблюдаемого небесного тела. Существуют особые методы определения расстояний, в которых учитываются физические свойства рассматриваемых объектов. Так как мы говорим о математике в астрономии, мы опишем только один метод, применимый к разным объектам, который часто используется в астрономии и заключается в измерении расстояний при помощи параллакса.

Параллакс — это изменение положения объекта относительно точки отсчета при изменении положения наблюдателя. Это явление знакомо каждому из нас. Делая снимок фотоаппаратом, видоискатель которого расположен на некотором расстоянии от объектива, мы увидим, что изображение не совпадает с тем, что получилось на фотографии. В кадр может не попасть человек, стоящий с краю, или мы можем случайно «обрезать» кому-то ноги. Это происходит потому, что в видоискатель мы видим не совсем то, что попадает в камеру через объектив.