Роза Мария Рос - Мир математики. т.30. Музыка сфер. Астрономия и математика

Четыре телескопа, образующие VLT (Very Large Telescope — англ. «очень большой телескоп») на Серро-Параналь в Чили. Телескопы больших размеров имеют альтазимутальную монтировку, так как она более устойчива. При использовании этих телескопов следить за небесными телами очень удобно — движением монтировки управляют компьютеры. Сегодня романтический образ астронома, приникшего к телескопу, ушел в прошлое, ведь ученые во время наблюдений смотрят на экран компьютера.

Два любительских телескопа с различными монтировками: слева — телескоп с экваториальной монтировкой, к которой можно подключить мотор для компенсации вращения; справа — телескоп с альт-азимутальной монтировкой.

* * *

При определении параллакса рассматривается новая единица длины — парсек.

Парсек — это расстояние, с которого одна астрономическая единица (напомним, что она равняется 150 млн километров) видна под углом в одну угловую секунду. Парсек эквивалентен 30,9 млрд километров, или, что аналогично, 3,26 светового года.

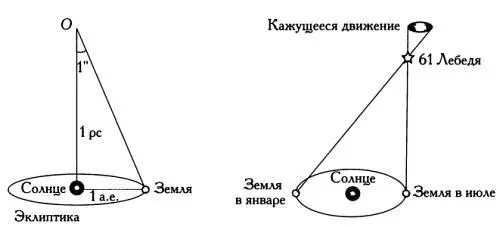
Один парсек соответствует параллаксу величиной в одну угловую секунду. Справа — годовой параллакс звезды 61 Лебедя.

Эта единица и кратные ей широко применяются в астрономии: килопарсек (тысяча парсек) — для измерения расстояний в масштабах галактик, мегапарсек (миллион парсек) — для измерения межгалактических расстояний (однако эти расстояния слишком велики, чтобы на них можно было наблюдать реальный параллакс).

Параллакс был известен уже древнегреческим астрономам, однако они не располагали измерительными инструментами необходимой точности для наблюдения годового параллакса, поэтому пришли к выводу: Земля неподвижна относительно Солнца.

Первым определил параллакс звезды (это была звезда 61 созвездия Лебедя) немецкий математик и астроном Фридрих Вильгельм Бессель в 1838 году. Чтобы представить, насколько мал параллакс даже ближайшей к нам звезды, рассмотрим ближайшую к Земле звездную систему Альфа Центавра. От Проксима Центавра, ближайшей к нам звезды, нас отделяет примерно 40 млрд километров, или 4,3 световых года. Следовательно, параллакс этой звезды меньше одной угловой секунды и равен 0,765” — меньше чем 1/3600 часть градуса, иными словами, 1/3600 части угла, под которым виден мизинец на вытянутой руке.

Чем больше расстояние, тем меньше параллакс, и ошибки измерения становятся всё более значимыми: на дистанциях, превышающих 100 световых лет, определить расстояния между звездами на основе годового параллакса уже нельзя.

* * *

ФРИДРИХ ВИЛЬГЕЛЬМ БЕССЕЛЬ (1784–1846)

Немецкий математик и астроном Фридрих Вильгельм Бессель родился в Миндене, был главой Кёнигсбергской обсерватории, описал так называемые функции Бесселя (открытые Даниилом Бернулли), занимался вычислениями орбит и положений небесных тел, изучал аберрации и рефракцию света в атмосфере. Он начал работу над решением сферических многоугольников и вывел известные формулы Бесселя, в том числе для решения уже упомянутого треугольника «полюс — зенит — звезда». Ученому удалось достичь высокой точности измерений и в 1838 году определить годовой параллакс звезды 61 Лебедя по итогам 18 месяцев наблюдений. В 1844 году, анализируя положение Сириуса и Проциона, он показал, что движение этих звезд можно объяснить только присутствием невидимого тела, под действием которого они смещаются с орбиты. Бессель даже рассчитал орбиту звезды Сириус В, которая была открыта лишь в 1862 году, а также звезды-спутника Проциона, открытой в 1895 году. Кроме всего прочего, Бессель известен благодаря публикации каталога, в котором приведены точные координаты 75 тысяч звезд, наблюдаемых из Северного полушария.

Портрет Фридриха Вильгельма Бесселяи изображение звезды Сириус А (большая звезда) и Сириус В (малая звезда, расположенная внизу слева), полученное космическим телескопом «Хаббл».

* * *

Помимо парсеков и кратных им единиц, которые мы определили выше, также используются световые года (св. г). Один световой год равен расстоянию, которое свет проходит за один год. Так как скорость света составляет 300 000 километров в секунду, световой год равен 9,46 трлн километров. Если в качестве точки отсчета используется Солнечная система, то, как вы уже знаете, в качестве единицы длины выступает астрономическая единица, равная 150 млн километров. Мы не способны представить себе расстояния в миллиарды километров, однако будет намного понятнее, если мы скажем, что Юпитер находится в 5 раз дальше от Солнца, чем Земля, то есть на расстоянии в 5 астрономических единиц (а. е.), а Сатурн — на расстоянии в 10 а. е.

Выбор подходящих единиц измерения позволяет упростить работу и лучше понять полученные результаты. Ярким подтверждением этому служит правило Тициуса — Боде, согласно которому расстояния между планетами Солнечной системы связаны фиксированным соотношением. С открытием этого правила началась настоящая охота за новыми небесными телами.

Правило Тициуса — Боде предложил Иоганн Даниэль Тициус в 1766 году, однако длительное время его авторство приписывалось главе Берлинской обсерватории Иоганну Элерту Боде, усилиями которого оно стало широко известным.

Иоганн Даниэль Тициус(слева) и Иоганн Элерт Боде.

Правило Тициуса — Боде можно представить в виде последовательности, общий член которой описывается следующим образом:

а n= 0,4+ 0,3∙ 2 n-2для n= 2,3,4… При n= 1 а 1= 0,4.

Следовательно, это правило описывает последовательность планет, удаленных друг от друга на следующие расстояния.

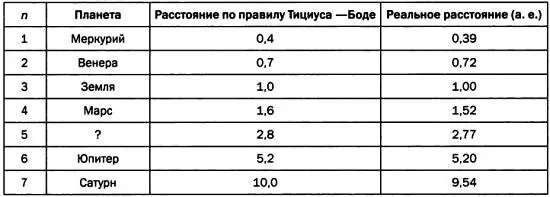
Последовательность планет Солнечной системы, известных в конце XVIII века, описываемая правилом Тициуса — Боде.

Как видите, в первом приближении это правило достаточно точное. В классической формулировке знаменатель прогрессии равен 2, однако более точные результаты достигаются при использовании значения 1,71.