Карлос Мадрид - Мир математики. т.32. Бабочка и ураган. Теория хаоса и глобальное потепление

* * *

Рассмотрим теперь логистическое отображение Мэя, которое задается следующим уравнением в конечных разностях:

х n+1= kх n(1 — х n).

Иными словами, для данного начального условия хна интервале между 0 и 1 орбита х рассчитывается путем последовательного вычисления значений функции f( х) = kx(1 — х), где k— параметр, больший 1, но меньший 4. Поведение логистической системы, названной так потому, что она используется для моделирования динамики численности определенных популяций, удивительным образом зависит от значения k. Если k меньше некоторого критического значения, которое, по оценкам, составляет 3,569945…, то траектории будут иметь правильную форму. При превышении этого критического значения траектории будут стремиться к хаосу. Эта дискретная динамическая система четко показывает, что простые математические действия могут обладать неожиданно сложными свойствами.

Функция f( х) является функцией второй степени:

f( х) = kx(1 — х) = kx— kx 2.

Иными словами, f( х) — нелинейная функция, и именно эта нелинейность делает возможным хаотическое поведение: в силу нелинейности небольшие отклонения начальных условий могут приводить к значительным изменениям.

Изучим динамику логистического отображения для значений k, меньших критического, к примеру для k= 2. Примем в качестве начального условия x 0 = 0,8 и определим его орбиту с помощью калькулятора:

x 1= f(х 0) = 2 х 0(1 — х 0) = 2∙0,8∙(1 — 0,8) = 2∙0,8∙0,2 = 0,32

х 2= f(х 1) = 2х 1(1 — х 1) = 2∙0,32∙(1 — 0,32) = 2∙0,32∙0,68 = 0,4352

х 3= f(х 2) = 2х 2(1 — х 2) = 2∙0,4352∙(1 — 0,4352) = 2∙0,4352∙0,5648 = 0,49160192.

Теперь, когда мы знаем, как рассчитываются первые члены орбиты, вычислим

следующие члены напрямую:

х 4= 0,4998589…

х 5= 0,4999998…

х 6= 0,4999999…

…

Обратите внимание на полученные значения. Что вы видите? Они последовательно приближаются к 0,5. Рассматриваемая траектория четко приближается к пределу — точечному аттрактору, расположенному в точке 0,5. Ради любопытства вычислим орбиту точки 0,5: так как f (0,5) = 2∙0,5∙(1 — 0,5) = 22424∙0,5∙0,5 = = 0,5, орбита этой точки будет стационарной (значения функции всегда будут равны 0,5). Следовательно, орбита точки 0,8 сходится к точке равновесия.

Рассмотрим, как наша траектория сходится к этой фиксированной точке, геометрически. Используем компьютерную программу, чтобы показать, как изменяются значения орбиты (представленные на вертикальной оси) с ростом числа итераций (откладываются на горизонтальной оси).

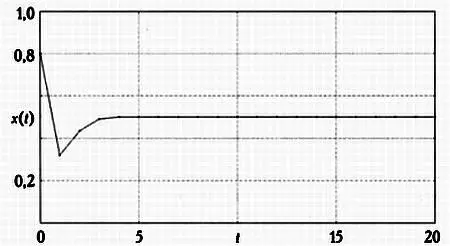
Нетрудно видеть, что значения орбиты очень быстро стабилизируются в окрестности точки 0,5, что мы уже вычислили при помощи калькулятора.

Далее будем изображать орбиту точки на так называемой диаграмме-паутине.

Построив график f( х) = 2 х(1 — х) (он будет представлять собой параболу, так как f( х) — функция второй степени), рассмотрим начальное условие x 0= 0,8. Далее определим орбиту этой точки графически. Проведем вертикальную линию через точку с абсциссой x 0 = 0,8 до пересечения с параболой — графиком функции f( x).

Затем из точки пересечения этой линии с параболой проведем горизонтальную линию до пересечения с диагональю у = х. Полученная абсцисса (координата на горизонтальной оси) будет указывать положение точки пересечения построенной линии с диагональю и будет соответствовать х 1Далее будем смещаться вертикально (вверх или вниз), пока вновь не пересечем график f( х). Повторив описанные выше действия, получим ломаную линию. Абсциссами ее вертикальных отрезков будут x 0, х 1, х 2, х 3. Эта ломаная линия укажет, куда будет стремиться орбита x 0.

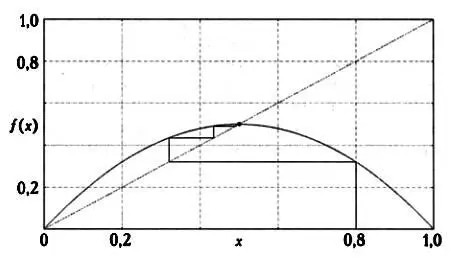
На этом графике можно видеть, как «паутина» точки x 0= 0,8 сходится к фиксированной точке, в которой пересекаются парабола — график функции f( х) — и прямая — график функции у= х. Как и следовало ожидать, этой фиксированной точкой будет точка 0,5.

Повторим описанные выше действия для другого значения параметра k. Примем его равным не 2, а 3,1. Орбита начальной точки x 0= 0,8 будет выглядеть так.

При значениях k, больших 3, происходит нечто удивительное: хотя движение по-прежнему будет оставаться правильным, орбита точки 0,8 уже не будет стремиться к какой-то одной точке. Вместо этого она будет колебаться между значениями 0,56 и 0,76. Точечный аттрактор 0,5 словно бы разделился на две точки с координатами 0,56 и 0,76. По сути, это пример орбиты с периодом, равным 2, так называемого 2-цикла, так как мы видим два точечных аттрактора. Новая паутина, которая будет порождать уже не точку, а квадрат, выглядит так.

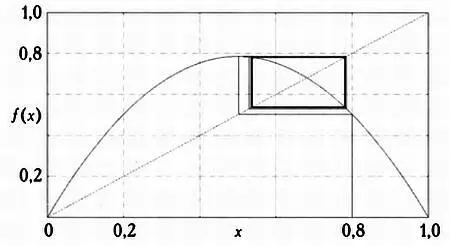
Продолжим увеличивать значения kи рассмотрим k = 3,5. Орбита x 0= 0,8 будет выглядеть так.

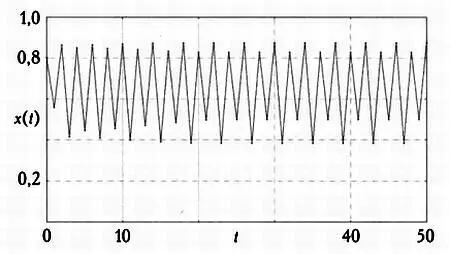
Теперь орбита будет колебаться между четырьмя точками. Их координаты приблизительно равны 0,39, 0,51, 0,82 и 0,86. Это уже 4-цикл, так как одни и те же значения будут повторяться каждые четыре шага. Кажется, что с увеличением kпериоды будут удваиваться: 1, 2, 4. Сначала мы наблюдали единственный точечный аттрактор, затем — два, теперь — четыре. Логично предположить, что далее их число будет равняться восьми, шестнадцати, тридцати двум и так далее. Наблюдаемая динамика уже не столь проста, однако ее по-прежнему можно назвать более или менее регулярной.

Позднее мы рассмотрим это необычное удвоение периода еще раз, а пока ограничимся тем, что изобразим новую паутину, образованную двумя основными квадратами.

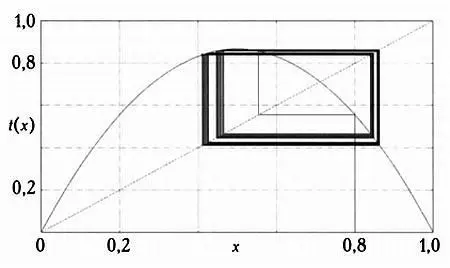
И наконец, осмелимся превысить критическое значение 3,569945. Рассмотрим k= 3,9. Ситуация радикально изменится. Орбита x 0= 0,8 будет выглядеть так.

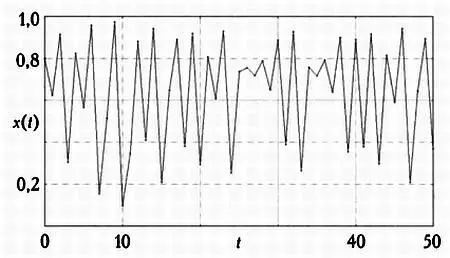
Орбита стала хаотической! В ней больше не наблюдается никаких закономерностей. Она даже не является квазипериодической, а «прыгает» с одного места на другое и кажется случайной. А что, если мы рассмотрим k= 4?