Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

История же подлинно математического филлотаксиса, в противоположность чисто описательному подходу, начинается лишь в XIX веке в работах ботаника Карла Фридриха Шимпера (вышли в свет в 1830 году), его друга Александера Брауна (1835) и кристаллографа Огюста Браве и его брата-ботаника Луи (1837). Эти ученые обнаружили общее правило, согласно которому соотношения, описывающие филлотаксис, можно выразить дробями, состоящими из членов последовательности Фибоначчи (например, 2/5 или 3/8), а также отметили, что в парастихиях сосновых шишек и ананасов также проявляются закономерности, описываемые числами Фибоначчи.

И в самом деле, нет прелестнее иллюстрации филлотаксиса на основе чисел Фибоначчи, чем ананас (рис. 32). Каждая шестиугольная чешуйка на поверхности ананаса входит в три различные спирали. На рисунке хорошо видны один из восьми параллельных рядов, которые полого поднимаются из левого нижнего угла в правый верхний, один из тринадцати параллельных рядов, которые более круто поднимаются из правого нижнего угла в левый верхний, и один из двадцати одного параллельного ряда, которые поднимаются очень круто (тоже из левого нижнего угла в правый верхний). На поверхности у большинства ананасов видны пять, восемь, тринадцать или двадцать одна спираль разной степени крутизны. Все это числа Фибоначчи.

Рис. 32

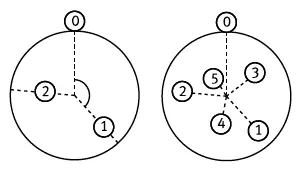
Рис. 33

Откуда растения знают, что нужно расставлять листья по закономерностям Фибоначчи? Зона роста у растения расположены на верхушке стебля и называется «меристема» – она конической формы и заостряется кверху. Листья, которые отстоят от меристемы дальше всего, то есть самые старые, если смотреть сверху, дальше всего отходят от середины стебля, поскольку и сам стебель там толще. На рис. 33 показан подобный вид на стебель сверху, а листья пронумерованы в порядке появления. Лист номер 0 появился первым и теперь находится в самом низу, дальше всех от меристемы, и отстоит дальше всех от середины стебля. Важную роль такого представления для понимания сущности филлотаксиса первым подчеркнул ботаник А. Г. Черч в своей книге «Связь филлотаксиса с законами механики» ( A . H. Church . On the Relation of Phyllotaxis to Mechanical Laws, 1904). Если мы представим себе кривую, которая на рис. 33 соединяет листья с 0 по 5, то обнаружим, что листья последовательно вырастают вдоль туго закрученной спирали – ее называют золотой спиралью. Важная характеристика расположения листьев – угол между линиями, соединяющими центр стебля с последовательно вырастающими листьями. Одно из открытий братьев Браве в 1837 году и состояло в том, что новые листья растут примерно под одним и тем же углом по кругу и что этот угол (так называемый угол расхождения) обычно близок к 137,5 градусам. Сейчас я вас изумлю: это значение тоже определяется золотым сечением! Если поделить полный круг, то есть 360 градусов, на φ, получится 222,5 градуса. Поскольку это больше половины круга (180 градусов), лучше измерять этот угол по оставшемуся сегменту круга. То есть нам надо вычесть 222,5 из 360 – и мы получим наблюдаемый угол в 137,5 градусов (иногда его называют золотым углом).

В 1907 году была опубликована революционная работа немецкого математика Г. ван Итерсона, где доказывалось, что если тесно расставить последовательные точки, разделенные под углом в 137,5 градусов, на туго свернутой спирали, то глаз будет выхватывать одно семейство спиральных узоров, которые закручиваются по часовой стрелке, и другое – против часовой. Количество спиралей в этих семействах – это обычно два соседних числа Фибоначчи, поскольку их отношение стремится к золотому сечению. Такие спирали, свивающиеся в противоположные стороны, особенно наглядно заметны в расположении семечек подсолнуха. Если рассмотреть цветок подсолнуха (рис. 34), можно отметить, что семечки образуют спиральные узоры и по часовой стрелке, и против. Очевидно, что семечки растут так, чтобы горизонтальное пространство распределялось между ними оптимально. Количество спиралей зависит, как правило, от размера цветка. Чаще всего их 34 в одну сторону и 55 в другую, однако ученым попадались и подсолнухи с соотношением количества спиралей 89/55, 144/89 и даже (по меньшей мере один, о котором одна семейная пара из Вермонта написала в 1951 году в журнал « Scientific American ») 233/144. Все это, конечно, соотношения соседних чисел Фибоначчи. У самых крупных подсолнухов структура меняется от центра к окружности – переходит от одной пары соседних чисел Фибоначчи к следующей.

Рис. 34

Числа Фибоначчи и связь с золотым сечением прослеживается также в числе и расположении лепестков. Иные люди даже доверяют свою жизнь, по крайней мере, символически, количеству лепестков ромашки, дабы решить животрепещущий вопрос «любит – не любит». У большинства полевых ромашек лепестков 13, 21 или 34 – и все это числа Фибоначчи (вот было бы славно заранее знать, четное или нечетное количество лепестков у попавшейся вам ромашки!). Количество лепестков отражает всего-навсего количество спиралей в одном из семейств.

Прелестное расположение лепестков розы также основано на золотом сечении. Если препарировать розу, снимая по лепестку, станет видно, что ее многочисленные, тесно прижатые друг к другу лепестки крепятся определенным образом. На рис. 35 приводится схема, где лепестки пронумерованы. Углы, определяющие положение лепестков (в долях окружности) – это дробная часть произведений φ на целые числа. Лепесток 1 расположен в 0,618 оборота от лепестка 0 (дробная часть 1 × φ), лепесток 2 – в 0,236 оборота от лепестка 1 (дробная часть 2 × φ) и т. д.

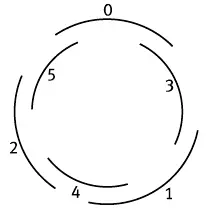
Рис. 35

Это описание показывает, что загадка филлотаксиса, насчитывающая уже 2300 лет, сводится к простому вопросу: почему последовательные листья разделены золотым углом в 137,5 градусов? Попытки найти ответ на этот вопрос идут, так сказать, под двумя соусами: теории, сосредоточенные на геометрии этой конфигурации и на простых математические законах, которые могли бы породить такую геометрию, с одной стороны, и модели, ищущие, какая движущая сила стоит за наблюдаемым поведением растений, с другой. Основные труды первого типа, авторами которых были, в частности, математики Гарольд С. М. Коксетер и И. Адлер и кристаллограф Н. Ривье, показывают, что почки, расположенные вдоль золотой спирали и разделенные золотым углом, упакованы экономичнее всего. Это легко понять. Если бы угол расхождения был, скажем, 120 градусов (360/3) или представлял собой любую другую рациональную долю 360 градусов, листья торчали бы в три стороны, а между ними бы оставалось много пустого места. С другой стороны, иррациональная доля 360 градусов вроде золотого угла обеспечивает, что не будет ни одного направления, которое листья «предпочли бы», и почки будут равномерно и экономно занимать все пространство. Однако золотой угол, оказывается, даже лучше любой другой иррациональной доли угла в 360 градусов, поскольку золотое сечение – самое иррациональное из всех иррациональных чисел, а в каком смысле, мы сейчас увидим. Вспомним, что золотое сечение равно непрерывной дроби, составленной исключительно из единиц. Эта непрерывная дробь сходится медленнее любой другой непрерывной дроби. Иначе говоря, выразить золотое сечение дробью еще труднее, чем любое другое иррациональное число.