Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Фибоначчи так знаменит в наши дни, поскольку применение чисел Фибоначчи отнюдь не сводится к разведению кроликов. Кстати, название этого раздела подсказала цитата из «Естественной истории интеллекта» Ральфа Уолдо Эмерсона, вышедшей в свет в 1893 году. Эмерсон говорит: «Все помыслы черепахи – лишь о черепахах, а кролика – о кроликах». С последовательностью Фибоначчи мы еще встретимся при изучении поразительно разнообразных явлений, на первый взгляд никак не связанных друг с другом.

Для начала рассмотрим явление, пожалуй, предельно далекое от генеалогии кроликов – оптику, науку о том, как распространяются лучи света. Предположим, у нас есть две стеклянные пластины, сделанные из стекла разного сорта (с разными показателями преломления света или «индексами рефракции»), и мы поставили их вплотную друг к другу (как на рис. 28, а ). Если мы посветим сквозь пластины, лучи света в принципе могут отразиться внутри от четырех отражающих поверхностей и лишь затем выйти наружу (рис. 28, а ). А точнее, они могут либо пройти сквозь стекло, вообще не отразившись, либо, прежде чем выйти наружу, отразиться внутри конструкции один, два, три и т. д. раз – потенциально число отражений может быть и бесконечным. Законы оптики допускают все варианты развития событий. Если внутренних отражений вообще не было, на выходе будет только один луч (рис. 28, b ). Если рассмотреть все варианты, при которых лучи претерпевают ровно одно внутреннее отражение (рис. 28, с), на выходе будет два луча, поскольку тогда лучи могут пройти двумя путями. При рассмотрении всех вариантов, когда внутренних отражений будет два, на выходе будет три луча (рис. 28, d ), пять лучей – для трех внутренних отражений (рис. 28, е), восемь – если луч отразится четырежды (рис. 28, f ), тринадцать – для пяти отражений (рис. 28, g ) и т. д. Количество лучей на выходе – 1, 2, 3, 5, 8, 13 … – это последовательность Фибоначчи.

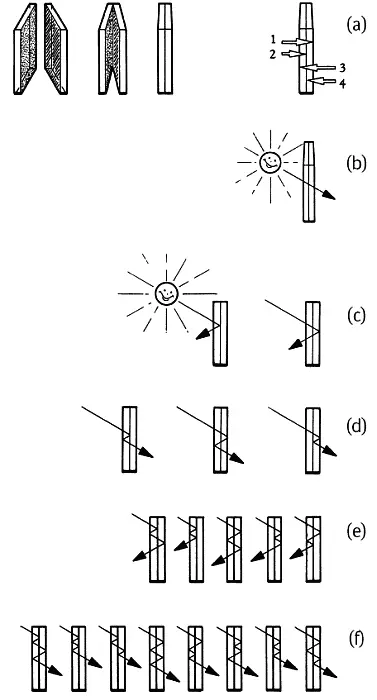
Рис. 28

А теперь рассмотрим еще одну задачу, совершенно иную. Ребенок взбирается по лестнице. Максимальное количество ступеней, которые он может одолеть за раз, – две; то есть он может за один шаг подняться либо на одну, либо на две ступени. Всего ступеней n . Сколькими способами С n ребенок может подняться по лестнице? Если ступеней только одна, то есть n = 1, очевидно, способ только один: С 1 = 1. Если ступеней две, ребенок может либо подняться сразу на две ступеньки, либо преодолеть их по одной, то есть способов два: С 2 = 2. Если ступеней три, способов подняться три: 1 + 1 +1, 1 + 2, 2 + 1, следовательно, С 3 = 3. Если ступеней четыре, количество способов возрастает до С 4 = 5: 1 + 1 + 1 + 1, 1 + 2 + 1, 1 + 1 + 2, 2 + l + l , 2 + 2. Для пяти ступеней способов уже С 5= 8: l + 1 + l + l + l , 1 + 1 + 1 + 2, 1 + 1 + 2 + 1, 1 + 2 + 1 + 1, 2 + 1 + 1 + 1, 2 + 2 + 1, 2 + 1 + 2, 1 + 2 + 2. Оказывается, количество вариантов l , 2, 3, 5, 8 … снова составляет последовательность Фибоначчи.

Наконец, исследуем генеалогическое древо самца пчелы – трутня. В трутней превращаются неоплодотворенные яйца пчел-работниц. То есть у трутня нет отца, только мать. С другой стороны, яйца пчелы-царицы оплодотворяются трутнями, и из них получаются самки (рабочие пчелы или царицы). То есть у рабочей пчелы есть и мать, и отец. Итак, у одного трутня есть один родитель, мать, одна пара бабушек и дедушек – родители матери, двое прабабушек и прадедушка, всего трое (мать и отец бабушки и мать дедушки), пять прапрабабушек и прапрадедушек (двое на каждую прабабушку и мать прадедушки) и т. д. То есть число ветвей на генеалогическом древе трутня составляет 1, 1, 2, 3, 5 – снова последовательность Фибоначчи. Схему такого генеалогического древа см. на рис. 29.

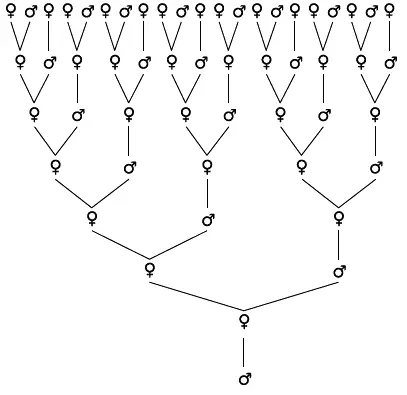
Рис. 29

Все это очень занимательно: одна и та же последовательность чисел относится и к кроликам, и к оптике, и к ступенькам лестницы, и к предкам трутня; но какое отношение числа Фибоначчи имеют к золотому сечению?

Снова рассмотрим последовательность Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 – и на сей раз посмотрим на отношения последовательных членов этого ряда (вычислять будем до шестого знака после запятой):

1/1 = 1,000000

2/1 = 2,000000

3/2 = 1,500000

5/3 = 1,666666

8/5 = 1,6000001

3/8 = 1,625000

21/13 = 1,615385

34/21 = 1,619048

55/34 = 1,617647

89/55 = 1,6180561

44/89 = 1,617978

233/144 = 1,618056

377/233 = 1,618026

610/377 = 1,618037

987/610 = 1,618033

Узнаете это число? Чем дальше мы продвинемся по последовательности Фибоначчи, тем ближе отношение двух соседних чисел Фибоначчи будет колебаться (то чуть больше, то чуть меньше) вокруг золотого сечения, неуклонно приближаясь к нему. Если обозначить n -ный член последовательности Фибоначчи как F n , а следующий за ним – как F n +1, то суть нашего открытия состоит в том, что чем больше n , тем ближе отношение F n / F n +1к числу φ. Это свойство чисел Фибоначчи открыл в 1611 году знаменитый немецкий астроном Иоганн Кеплер (а возможно, его опередил неизвестный итальянский математик), однако прошло более ста лет, прежде чем связь между числами Фибоначчи и золотым сечением была доказана, да и то не до конца, шотландским математиком Робертом Симсоном (1687–1768). Кстати, Кеплер, очевидно, открыл последовательность Фибоначчи совершенно самостоятельно, а не из «Книги абака».

Но почему члены последовательности, выведенной из схемы разведения кроликов, подводят нас к соотношению, выведенному из деления отрезка? Чтобы понять эту связь, придется вернуться к поразительной непрерывной дроби, с которой мы познакомились в главе 4. Вспомним, что мы обнаружили, что золотое сечение можно записать в виде:

В принципе, можно вычислить значение φ методом последовательных приближений: прерывая непрерывную дробь все ниже и ниже. Предположим, мы именно так и поступим. Тогда у нас получится целый ряд значений (напомню: 1 к a / b – это все равно, что b / a ).

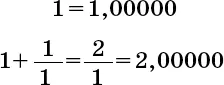
Иными словами, последовательные приближения, при помощи которых мы ищем золотое сечение, в точности равны соотношениям чисел Фибоначчи. Ничего удивительного, что чем дальше мы продвигаемся по последовательности, тем ближе они сходятся к золотому сечению. Это качество прекрасно описано в книге «О росте и форме» знаменитого натуралиста сэра Д’Арси Уэнтворта Томпсона (1860–1948) ( Sir D ’ Arcy Wentworth Thompson . On Growth and Form). Вот как он пишет о числах Фибоначчи: «Один мой друг, сведущий в математике, пишет мне б этих прославленных, поразительных числах: “Вся романтика непрерывных дробей, линейных рекурретнтых последовательностей… все это есть в них, и они – источник бесконечного интереса; как увлекательно наблюдать, с каким рвением они стремятся достичь недостижимого – например, золотого сечения; а ведь это всего лишь одно из сотен подобных соотношений”». Кстати, сходимость золотого сечения объясняет математический фокус, который я показал вам в главе 4. Если определить последовательность чисел так, что каждый член последовательности (начиная с третьего) равен сумме двух предшествующих, то с каких бы двух чисел вы ни начали, если зайти по последовательности достаточно далеко, отношение двух последовательных членов будет приближаться к золотому сечению.