Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

Существовало две системы обозначений. В первой за основу было взято вертикальное положение палочек, что можно видеть на следующей иллюстрации, где слева направо записаны числа от 1 до 9.

Во второй системе за основу было взято горизонтальное положение палочек, как показано далее. Здесь тоже представлены числа от 1 до 9.

Эта система счисления использовалась на табличках, где для представления чисел цифры записывались по-разрядно. Например, число 4508 на такой табличке записывалось следующим образом.

Как вы можете видеть, в записи чисел участвовали обе системы одновременно: вертикально расположенные палочки обозначали единицы, сотни и так далее; палочки, расположенные горизонтально, — десятки, тысячи и следующие разряды. Если одна из цифр равнялась нулю, соответствующая позиция оставалась пустой, как вы можете видеть на примере записи числа 4508. Аналогичным образом записывались отрицательные числа. Положительные и отрицательные числа различались цветом палочек: для записи положительных чисел использовались красные палочки, для записи отрицательных — черные.

Арифметические действия выполнялись на той же табличке с теми же палочками. Сложение и вычитание производились путем добавления палочек или удаления их с доски. Были известны методы умножения и деления, а также алгоритмы выполнения других алгебраических операций, в частности нахождения корней многочленов.

Система вычислений с помощью палочек также появилась в Корее и Японии (точный период неизвестен). Известно, что эта система применялась в Японии в период правления императрицы Суйко (593–628) под названием санги.

Абак был известен в Китае начиная со II в. до н. э. под названием суаньпань. Китайский абак делился на две части: костяшки верхней части обозначали пять единиц (либо десять, сто и так далее), а каждая костяшка в нижней части обозначала единицу. Подобным образом на две части делился и римский абак. Учитывая длительную торговлю Римской империи с Китаем, некоторые исследователи всерьез полагают, что римский и китайский абак были созданы под влиянием друг друга.

Учитель объясняет ученикам китайской школы округа Чжэньцзян, как пользоваться абаком. 1938 год.

Китайский абак появился в Японии примерно в XVI веке и был известен как соробан. Он появился благодаря торговцам, однако его распространение было непростым. Лишь спустя много лет он был введен в школах и начал использоваться для решения сложных математических задач. В торговле соробан быстро заменил ранее применявшиеся устройства, однако они по-прежнему использовались в высшей математике.

Для обозначения цифр и в Китае, и в Японии (системы счисления в этих странах очень похожи) использовались девять идеограмм.

Для обозначения десятков, сотен, тысяч и следующих разрядов эти символы записывались рядом со следующими идеограммами:

При записи чисел использовались символы от 1 до 9 вместе с символами десятков, сотен и так далее. Например, число 10563 записывалось следующим образом:

что расшифровывается так:

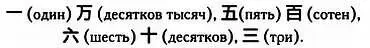
Следует упомянуть, что в отличие от системы, используемой в большинстве европейских языков, в основе которой лежит тысяча (10 3), в китайской системе в основе кратных величин лежит 10 4. Следовательно, 132000 записывается как 13·(104) + 2000.

В виде идеограмм это число будет представлено так:

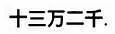
Китайцы разработали алгоритмы для вычисления числа π . Великий математик Лю Хуэй, живший около 300 года во времена царства Вэй, возникшего после распада империи Хань, первым создал метод вычисления числа π . Живший до него ученый и изобретатель Чжан Хэн(78—139) , который создал прибор для определения землетрясений за 1700 лет до появления первого сейсмографа, получил приближенное значение π , равное 3,1724. Также использовались значения 3,162 (корень из 10) и 3,156. В III веке астроном Вань Фань, живший в царстве У, использовал последнее значение, равное дроби 142/45.

Первый метод, использованный Лю Хуэем для нахождения приближенного значения π , заключался в бисекции многоугольников. С помощью многоугольника с 96 сторонами он вычислил, что π лежит в интервале между 3,141024 и 3,142708. Он использовал приближенное значение, равное 157/50, так как считал значение 3,14 достаточно точным.

Китайские марки, посвященные ученым Лю Хуэю(слева) и Чжану Хэну(справа).

Лю Хуэй использовал шестиугольник со стороной L , вписанный в окружность. Далее число сторон многоугольника последовательно удваивалось. Иными словами, сначала рассматривался шестиугольник, затем 12-угольник, далее — 24-угольник (24 = 12·2), 48-угольник (48 = 24·2) и так далее. На каждом шаге Лю Хуэй вычислял площадь многоугольника с N сторонами и длину стороны многоугольника с числом сторон, равным 2 N .

Будем обозначать за l длину стороны многоугольника с 2 N сторонами. Используем теорему Пифагора: для данного прямоугольного треугольника с гипотенузой h и двумя катетами длиной с 1 и с 2 выполняется равенство h 2= с 1 2+ с 2 2.

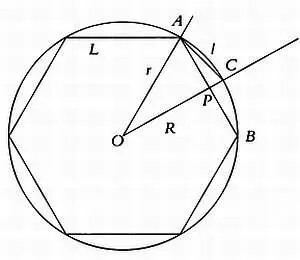
Вычисление длины стороны lпо известному значению L, где L— длина стороны шестиугольника, I — длина стороны 12-угольника,

О— центр окружности, Аи В— две вершины шестиугольника, С — новая вершина, Р— точка на стороне шестиугольника, равноудаленная от Аи В. Радиус окружности равен r, расстояние от центра до Р равно R.