Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

На рисунке обозначены центр окружности О и сторона шестиугольника (длиной L ). Ее концы обозначены А и В . Точки ОАВ определяют треугольник. Далее вычисления выполняются следующим образом.

Шаг 0. Будем рассматривать многоугольник с N = 6 сторонами, длина его стороны L известна.

Шаг 1. Разделим сторону АВ на две равные части. Обозначим середину стороны АВ точкой Р .

Шаг 2.Вычислим длину отрезка ОР и обозначим ее длину за R . Для этого применим теорему Пифагора. Нам известно, что гипотенуза треугольника ОАР равна r , один из катетов равен L /2, длина другого, которую мы хотим вычислить, равна R . По теореме Пифагора г 2= R 2+ ( L /2) 2. Отсюда имеем R 2= r 2— ( L /2) 2, следовательно

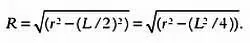
Шаг 3.Рассмотрим радиус окружности, который проходит через точку Р . Точка пересечения этого радиуса и окружности будет вершиной многоугольника с 2 N сторонами. Обозначим эту точку С . Зная R , мы можем вычислить длину отрезка PC . Обозначим ее за р . Так как длина ОС равна r , длина PC равна

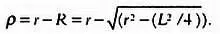
Шаг 4.Длину отрезка АС можно определить по теореме Пифагора. Как мы уже говорили, будем обозначать длину этого отрезка за l . В рассматриваемом прямоугольном треугольнике гипотенуза равна l , катеты — L /2 и р . Следовательно,

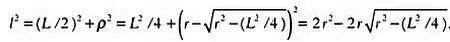
Шаг 5.Выразив l из последнего равенства, получим длину многоугольника с 2 N сторонами:

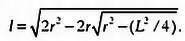
Шаг 6.Площадь многоугольника с N сторонами можно вычислить на основе площади треугольника ОАВ . Площадь многоугольника будет в N раз больше площади этого треугольника. Площадь треугольника ОАВ , очевидно, равна половине произведения его основания на высоту. Длина основания АВ равна L , высота равна R (это значение мы уже вычислили). Следовательно, площадь многоугольника равна

N ·площадь треугольника ОАВ = N ·( L · R )/2.

Шаг 7.Далее нужно вернуться к шагу 2 и принять N = 2 N, L = l . Чтобы определить значение π , нужно учесть, что площадь круга равна π·r 2. Следовательно, для r = 10 площадь круга равна π· 100.

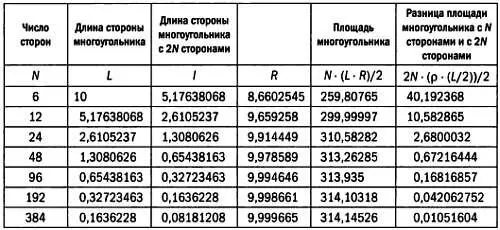
Если начать с r = 10 (в этом случае L = 10), с помощью вышеприведенного алгоритма мы получим значения площадей, представленные в таблице ниже. В этой таблице используется современная нотация, Лю Хуэй в своих расчетах применял дроби. Он заметил, что для данного многоугольника с 2 N сторонами длиной l , построенного на основе многоугольника с N сторонами длиной L , площадь круга (обозначим ее за С ) удовлетворяет следующему неравенству:

площадь (2 N ) < С < площадь (2 N ) + избыток.

Избыток в этом неравенстве соответствует 2 N треугольникам площадью р ·( L /2)/2. Напомним, что р = r — R . Получим значение избытка, равное 2· N ·( р ·( L /2))/2. Эти значения также приведены в таблице. Разница между площадью 96-угольника и 192-угольника очень мала, поэтому Лю Хуэй счел π = 3,14 достаточно точным.

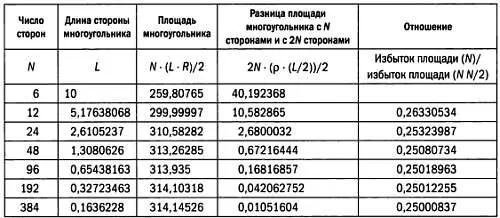
Лю Хуэй заметил, что между последовательными избытками наблюдается определенное соотношение. В частности, он установил, что отношение между данным и следующим избытком примерно равно 1/4 = 0,25. Эти отношения представлены в таблице ниже. Используя это отношение, он вычислил приближенное значение площади 3072-угольника и с его помощью получил более точную оценку числа π .

В качестве примера рассмотрим, как Лю Хуэй определил площадь 384-угольника на основе последнего значения площади, вычисленного им напрямую, — площади 192-угольника. Площадь 192-угольника равна 314,10318, избыток площади этого многоугольника по отношению к предыдущему равен 0,16816857. Далее Лю Хуэй вычислил разницу площадей 192-угольника и 384-угольника. Она составила 0,16816857·(1/4) = 0,042042144. Следовательно, площадь 384-угольника равна:

314,10318 + 0,16816857·0,25 = 314,14523.

Реальный избыток площади равен 0,042062752, площадь многоугольника равна 314,14526.

С помощью этого способа Лю Хуэй вычислил площадь 3072-угольника и получил приближенное значение π , равное 3927/1250 = 3,14159.

В 480 году этот метод был пересмотрен математиком и астрономом Цзу Чунчжи(429–500) , жившим во времена династии Ци. Использовав многоугольник с 12288 = 3·2 12сторонами, он определил, что π заключено между следующими значениями: 3,1415926 < π < 3,1415927. Он представил результат так:

π ~= 355/113. В течение 900 лет эта оценка оставалась наиболее точной.

История науки гласит, что индийская математика возникла в VII веке, когда в этой стране в качестве всеобщего языка уже использовался санскрит. Индия не была изолированной от Европы: индийцы поддерживали тесные контакты с греками, позднее с римлянами. Не следует забывать, что граница империи Александра Македонского проходила по долине реки Инд.

Хотя индийские ученые уделяли особое внимание астрономии, они занимались и математикой, которая играла важнейшую роль в развитии научной мысли. Любопытно, что индийцы не разделяли подход к науке, принятый в странах Востока, и не считали, что она обязательно должна иметь практическое применение. Стимулом развития индийской математики было получение знаний ради самих знаний. Несмотря на это, индийские ученые не слишком охотно приводили более или менее формальные доказательства своих методов и алгоритмов. Считается, что они обосновывали свои открытия, но найденные ими доказательства не сохранились.

Индийцы подробно изучили тригонометрию, особенно применительно к астрономическим расчетам и решениям неопределенных уравнений, а также алгебру и комбинаторику. По сути, понятие синуса и само слово «синус» впервые упоминаются в трактате по астрономии V века «Пайтамаха-сиддханта».

* * *

СИНУС

Как случилось, что для обозначения тригонометрической функции стало использоваться слово «синус»? Эта история берет начало в индийском трактате по астрономии под названием «Пайтамаха-сиддханта», в котором приводится таблица джайя-ардха — «измерение струн», использовавшаяся в астрономических расчетах. Этот термин вновь упоминается в труде «Ариабхатия» индийского математика Ариабхаты, который обозначал его как «джайя», или «джива». Арабы перевели это слово как «джиба», но так как в арабском отсутствуют отдельные буквы для обозначения гласных, то это слово записывалось как джб. При более позднем прочтении случайно или умышленно джб было прочитано как джаиб, что означало «грудь» или «пазуха», а переводчики на латынь использовали слово «синус», означавшее «пазуха», «складка на тоге», а также «залив». Этот термин используется не только в романских языках: даже английское слово sine имеет латинское происхождение.