Бизенц Торра - Том 15. От абака к цифровой революции. Алгоритмы и вычисления

Помимо табличек, римляне также использовали разновидность абака — металлические или деревянные таблички с бороздками, в которых располагались небольшие камни, обозначавшие числа. Может показаться парадоксальным, но эти камушки сыграли большую роль в математике: латинское слово «камень» звучало как calx , а от его уменьшительной формы, calculus , означавшей «небольшой камень», или «камушек», в частности, происходит современное слово «калькулятор».

У греческих математиков в Римской империи не нашлось достойных последователей. Великие открытия, совершенные в течение этого длительного периода продолжительностью почти в восемь столетий, были заслугами математиков Древней Греции. В то время одним из важнейших научных центров была Александрия, где располагались музей и библиотека. Некоторые известные греческие математики, жившие в эпоху заката Римской империи, работали именно в Александрии.

Уже упомянутый Папп Александрийский, живший в начале IV века, попытался обновить греческую математику и создал сборник комментариев и толкований классических текстов. В его трудах приведены более подробные доказательства, которые помогают читателю понять труды древних. К сожалению, его идея окончилась неудачей: за ним последовали лишь немногие известные математики.

* * *

ГИПАТИЯ АЛЕКСАНДРИЙСКАЯ

Гипатия(ок. 370–415) — дочь математика и философа Теона Александрийского, от которого она унаследовала талант и любовь к наукам. Она была язычницей в то время, когда официальной религией Римской империи уже было христианство, а язычество преследовалось. Несмотря на это, Гипатию не затронули религиозные противоречия, и среди ее учеников был даже будущий епископ Синезий. Тем не менее в 415 году Гипатия оказалась вовлечена в политическое противостояние между христианским патриархом Кириллом и римским префектом Орестом, который был ее другом и учеником. Чтобы навредить Оресту, кто-то пустил слух, что Гипатия — ведьма, и она была зверски растерзана толпой во время Великого поста.

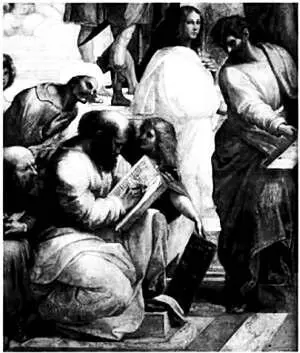
На этом фрагменте «Афинской школы» Рафаэля изображена Гипатия Александрийскаяв белой тунике.

* * *

Одним из немногих блестящих математиков, живших позднее Паппа, была знаменитая Гипатия, среди трудов которой выделяются комментарии к Аполлонию Пергскому («О конических сечениях») и к «Арифметике» Диофанта. Она также помогла отцу при написании комментариев к «Альмагесту» Птолемея. После убийства Гипатии в 415 году, отдавшей жизнь ради науки, и разрушения Александрийского музея и библиотеки в IV–VII веках (точное время неизвестно) наследие греческих математиков было предано огню и похоронено под руинами, откуда его бережно извлекли арабы.

Математика сыграла фундаментальную роль в истории Китая, полной научных и технических открытий, часто опережавших свое время. Со времен династии Хань (206 г. до н. э. — 220 г. н. э.) условием получения государственной должности была успешная сдача непростого экзамена, а не семейные связи, как можно было бы ожидать.

В таких экзаменах особое внимание уделялось классической китайской литературе, а также, что примечательно, математике. Может показаться невероятным, но эти экзамены сохранились до наших дней. Разумеется, их целью была не оценка творческих способностей в математике. Как правило, при подготовке к экзамену требовалось заучить определенные задачи и их решения. Логично, что в Китае разделяли типично восточные взгляды на науку, свойственные вавилонянам и египтянам, которые рассматривали науку с чисто практической точки зрения. Несмотря на это, ничто не могло помешать представителям столь богатой культуры совершить собственные математические открытия в поиске новых, более эффективных методов решения всё более и более сложных задач.

Важнейшим математическим трудом Древнего Китая является «Математика в девяти книгах». Jiu zhang suanshu (так звучит название этой книги на языке оригинала) — это классический труд, который использовали многие поколения китайских математиков вкупе с комментариями и аннотациями Лю Хуэя (III в. н. э.).

В 1983 году в гробнице 186 года до н. э. было найдено 190 бамбуковых пластинок с математическими текстами. Каждая пластинка имела 30 сантиметров в длину и 6–7 миллиметров в толщину. Всего на них было записано примерно 7000 иероглифов. Пластинки изначально были скреплены между собой по порядку и свернуты, однако на раскопках гробницы они были найдены в беспорядке, поскольку соединявшие их нити истлели от времени. Ученым пришлось немало поломать головы, чтобы восстановить исходный порядок расположения пластин.

Репродукция XVIII века одной из задач китайского математика Лю Хуэя, в которой требуется измерить высоту берега острова.

После того как текст книги был восстановлен, ученые подробно изучили его и поняли, что к ним в руки попал труд величайшей важности. Он содержал задачи различных типов, в которых требовалось рассчитать налог, вычислить объем и так далее. Несмотря на практическую направленность, в этих задачах интересным образом применялся, в частности, метод ложного положения, а также алгоритмы вычисления квадратных корней. Интерес представляют и формулировки задач, подчас аллегорические.

* * *

ЗАДАЧА ИЗ «МАТЕМАТИКИ В ДЕВЯТИ КНИГАХ»

Следующая задача, приведенная в свитках 34 и 35 «Математики в девяти книгах», может служить примером того, какие вопросы рассматривались в этой книге. Она звучит так: «Лиса, лесная кошка и собака должны заплатить на таможне 111 монет. Собака говорит кошке, а кошка говорит лисе: Твоя шкура вдвое дороже моей, ты должна заплатить в два раза больше”. Сколько должен заплатить каждый?»

* * *

Следующие части книги посвящены разделам китайской математики, относящимся к интересующей нас теме — к счету и системам счисления. Стоит отметить, что китайские математики совершили множество других важных открытий, которые не упоминаются в следующих главах, но тем не менее занимают важное место в истории математики. В частности, они разработали методы решения уравнений и геометрических задач о равенстве фигур.

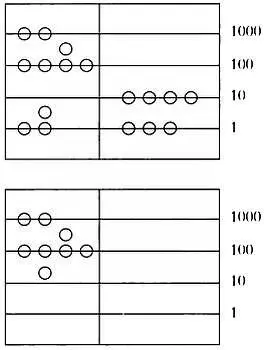
Древнейшая форма вычислений, которая бытовала в Древнем Китае, восходит к IV веку до н. э. Для вычислений использовались палочки, известные как суань 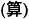или чоу 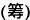. Со временем на смену этим палочкам пришел абак. Эти палочки, которые располагались горизонтально и вертикально, обозначали цифры от 1 до 9.