Хавьер Арбонес - Том 12. Числа-основа гармонии. Музыка и математика

Обертоны, выражающиеся степенями двойки (2, 4, 8, …), соответствуют октавам основного звука и усиливают его интенсивность. Обертоны, выражающиеся числами, кратными 3 (3, 6, 12, …), соотносятся с цепочкой квинт. Присутствие таких обертонов приводит к появлению назализованного тембра. Обертоны, выражающиеся числами ряда 5, 10, 20, …, соответствуют терциям основного звука и придают звуку теплоту. Наконец, обертоны, соответствующие диссонирующим интервалам, добавляют звуку шероховатость.

Первые попытки сконструировать электрический орган были предприняты свыше 100 лет назад. Пионерами в этом направлении были американец Таддеус Кэхилл(1867–1934) , который в 1900 году придумал телармониум; русский ученый Лев Термен(1896–1993) , который в 1924 году изобрел инструмент, носящий его имя, — терменвокс, и француз Морис Мартено(1898–1980) , усилиями которого в 1928 году свет увидел инструмент «волны Мартено». Эти открытия дали начало новому направлению развития технологий. Работы по созданию электронных музыкальных инструментов достигли пика после Второй мировой войны. В XX веке технологические открытия в области звука позволили глубоко изучить его природу и особенности, а также открыть эффективные способы синтеза звуков.

Для синтеза звука первым делом нужно его сгенерировать. Для этого используются два способа: в первом применяются отдельные источники для каждого из 12 звуков верхней октавы, во втором генерируется лишь самый высокий звук этой октавы, а оставшиеся 11 полутонов получаются путем электронных преобразований. После того как сформированы звуки верхней октавы, частоты звуков остальных октав получаются с помощью электронных делителей частоты делением частоты на 2.

Итак, базовый звук создан. Теперь можно изменять его различные параметры, что позволит добиться нужного звучания. Это ключевой момент: поискам синтетических звуков, максимально приближенных к реальным, сопутствует желание создавать совершенно новые, неповторимые звуки. Успехи в синтезе звуков, достигнутые в последнее время, охватывают различные аспекты. Некоторые заслуживают упоминания. Таковы, в частности, фильтры и усилители, которые обрабатывают обертоны и тем самым позволяют изменять тембр звука, сгенерированного осциллятором. Если звук не богат обертонами, его обогащают с помощью усилителей, генерирующих обертоны, частоты которых кратны частоте основного тона. Также применяются фильтры, позволяющие ограничить или подавить составляющие определенной частоты. Комбинирование обертонов используется для создания определенного тембра, что позволяет имитировать, например, звук трубы, скрипки или любого другого музыкального инструмента. Чаще всего используются следующие фильтры:

— фильтр нижних частот, подавляющий высокие частоты;

— фильтр верхних частот, подавляющий низкие частоты;

— полосовой фильтр, пропускающий частоты из определенного интервала;

— полосно-заграждающий фильтр, не пропускающий частоты в определенном интервале.

Все звуки, которые мы слышим в повседневной жизни, попадают в наши уши в виде волн, распространяющихся в воздухе, воде и других звукопроводящих средах. С момента изобретения фонографа Томасом Эдисоном в 1877 году были созданы различные аналоговые средства хранения и воспроизведения звука.

В аналоговых системах звук должен быть преобразован в последовательность электрических сигналов с помощью преобразователя, например микрофона. Эти сигналы, которые в конечном итоге будут фиксироваться и впоследствии воспроизводиться, могут быть преобразованы в звуковые волны с помощью другого преобразователя, например репродуктора.

* * *

«У МЭРИ БЫЛ БАРАШЕК» ИЛИ «В СВЕТЕ ЛУНЫ»?

До 2008 года первой в истории записью человеческого голоса считалась сделанная самим Томасом Эдисоном, который 21 ноября 1877 года прочитал стихотворение Mary had a little lamb («У Мэри был барашек») для проверки изобретенного им фонографа. Спустя несколько дней он впервые продемонстрировал свое изобретение на публике. Через год он запатентовал его и представил Французской академии наук. Члены Академии были настолько поражены увиденным, что сначала посчитали фонограф подделкой и заподозрили, что в зале сидит чревовещатель. Звуковые колебания записывались на оловянной фольге, обернутой поверх цилиндрического валика, который вращался вокруг своей оси. Позднее вместо олова стал использоваться воск. Звук записывался на фольге в виде спиралевидных дорожек, которые затем считывались и снова преобразовывались в звук.

Изначально фонограф использовался в качестве диктофона на предприятиях и в правительственных учреждениях. Сам Эдисон никогда не думал, что его изобретение будет широко использоваться для записи и воспроизведения музыки, и сначала даже запретил применять фонограф подобным образом. Однако музыкальный цилиндр распространился по всему миру, и в 1890-е годы ему на смену пришли плоские диски.

За 20 лет до первой записи Эдисона француз Эдуар Леон Скоп изобрел фоноавтограф, который мог записывать звуковые колебания, но не воспроизводил их. Записи фоноавтографа хранились в Библиотеке Конгресса США. В 2008 году группе исследователей удалось воспроизвести эти записи, датируемые 1860 годом. Они услышали известную французскую песню Au claire de la Lune («В свете луны») — первую в истории запись звука.

* * *

Аналогово-цифровое преобразование

Аналогово-цифровое преобразование выполняется посредством импульсно- кодовой модуляции сигналов (англ. РСМ — Pulse-Code Modulation ) аналогово-цифровым преобразователем (англ. ADC — Analog-to-Digital Converter ). Аналоговый звуковой сигнал легко представить в виде кривой, которую можно описать численно.

Аналогово-цифровое преобразование заключается в дискретизации этой кривой: сигнал замеряется с заданной частотой и разбивается на множество одинаковых интервалов. Чем больше число интервалов, тем ближе к исходному будет записанный и воспроизводимый сигнал и тем выше качество записанного звука. Это же происходит и в кино: чем больше кадров демонстрируется в секунду, тем плавнее выглядят движения на экране. Можно привести и другой пример: чем больше точек, лежащих на кривой, нам известно, тем точнее мы сможем восстановить исходную кривую.

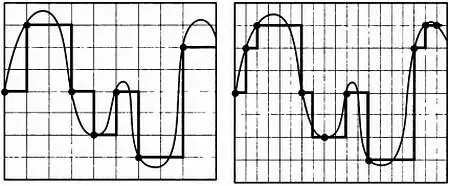
Чем больше число измерений (вертикальных линий) звука, тем ближе к исходной кривой будет ее представление в виде прямоугольников сетки.

По теореме Найквиста — Шеннона (в русскоязычной литературе теорема Котельникова) при определенных условиях аналоговый сигнал с максимальной частотой М может быть восстановлен однозначно и без потерь, если количество измерений в секунду превышает 2 М . Так как максимальная частота, которую необходимо зафиксировать, равняется 20000 Гц (это порог слышимости звука человеком), частота дискретизации при записи музыки на CD равна 44100 раз в секунду — эта величина несколько больше удвоенной максимальной частоты звука.