Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

е = 2,71828 18284 59045 23536 0287471135 26624 99757 54692 80835 55155 05841 72…

Теперь скажи мне: что нужно сделать, если ты захочешь получить вдвое большую площадь, то есть равную двум квадратным единицам?

— Здесь опять все пойдет в геометрической прогрессии, — отвечал Илюша. — Если нужно перенести единичную площадь направо, откладывая ее не от х = 1, а от х = е , то надо все площадочки-неделимые втиснуть в промежуток в е раз более тесный и, следовательно, расширять во столько же раз их основания.

Значит, я дойду до абсциссы е · е = е 2. Дальше будет то же самое. Когда я дойду от х = е до абсциссы х = е n , наберется площадь, равная n .

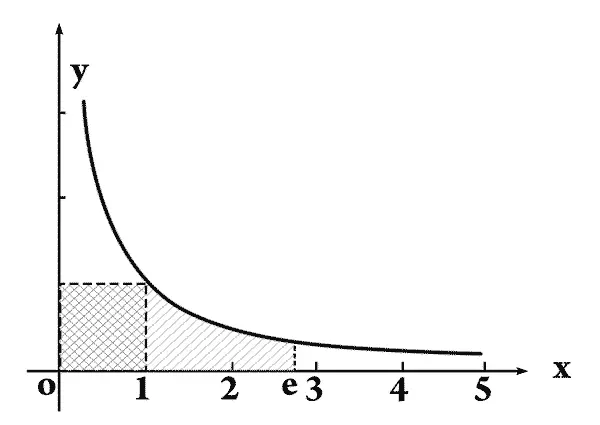
— Значит, — сказал Радикс, — числа, измеряющие величины гиперболических трапеций в обычной единице меры, будут…

— Логарифмами конечных абсцисс при основании е , — отвечал Илюша. — Так это ведь и есть натуральные логарифмы?

— 371 —

— Вот именно. И заметь, что это рассуждение дает нам в руки способ вычисления этих логарифмов для любых положительных чисел, что далеко не так просто сделать, если искать нужный показатель степени. Потому что вычислять с дробными степенями, как ты сам, вероятно, не раз замечал, не так уж весело. Здесь же можно просто отложить абсциссу, равную числу N , логарифм которого тебе нужен, и измерить площадь гиперболической трапеции от х = 1 до х = N .

— Но это уже будет геометрический способ. А потом как же быть с большими числами?

— На миллиметровой бумаге можно добиться довольно большой точности, а для больших чисел придется уже вычислять. Вспомни, как мы вычисляли площадь, ограниченную дугой параболы. Ты ведь и здесь можешь разбить интересующий тебя участок на большое число частей и вычислить (а не измерять непосредственно) сумму площадей соответствующих тоненьких прямоугольников. Это уже можно сделать с любой степенью точности, то есть той, какая понадобится.

Но есть и более удобные способы вычисления логарифмов.

— А какие же логарифмы применяются на самом деле,— спросил Илюша, — натуральные или какие-нибудь другие?

— Натуральные обладают целым рядом преимуществ перед остальными, и в математическом анализе применяются почти исключительно они. Но в практических вычислениях удобнее иметь дело с десятичными, для которых и составлены таблицы.

А если надо перейти от десятичных к натуральным или наоборот, то пользуются модулем перехода, о котором мы уже говорили. Чтобы получить десятичный логарифм, надо натуральный умножить на

M = 0,43429 44809 032518 276511 289189 1660508 2294397 005803 7675761 1445378 …

— 372 —

Это число называется модулем десятичных логарифмов.

— А нельзя ли десятичные логарифмы получить тоже как площади гиперболических трапеций?

— Конечно, можно. Перемена основания соответствует, как мы уже видели, просто перемене способа измерения площадей. Если ты в качестве единицы для измерения площадей выберешь основную гиперболическую трапецию, простирающуюся от х = 1 до х = 10, то как раз и получишь десятичные логарифмы. Так как единица измерения увеличилась, то площади будут выражаться меньшими числами, то есть десятичные логарифмы будут меньше натуральных, почему и модуль их меньше единицы.

— А почему обычные логарифмы — десятичные, а не какие-нибудь другие?

— Просто потому, что мы пользуемся десятеричной системой счисления. Древний халдей, вероятно, выбрал бы для основания не десять, а свое любимое число шестьдесят, если бы он додумался до логарифмов. А в десятеричной системе счисления сразу известны логарифмы чисел 10, 100, 1 000, 10 000 и т. д. Они равны 1, 2, 3, 4… Поэтому, умножая какое-нибудь число на десять, сто и так далее, сразу можно сказать, что десятичный логарифм этого числа увеличится на единицу, на два и прочее, а при делении будет наоборот. Это очень облегчает пользование таблицами.

Илюша помолчал минутку.

— А это что такое? — спросил доктор У. У. Уникурсальян.

— Вот что, — произнес он наконец, — мне кажется, что теперь я могу разобраться, почему при помощи логарифмов умножение заменяется сложением. Если взять гиперболическую площадку от х = 1 до х = n , то это будет логарифм числа n . Если к нему рядом приладить еще одну площадку величиной от х = 1 до х = m , то есть логарифм числа m , то, как мы уже делали раньше, придется вторую площадку растянуть от n до nm , удлинив абсциссу в m раз. Значит, тут конечные абсциссы (то есть числа) перемножаются, в то время как площади складываются. Вот теперь мне,

— 373 —

кажется, все ясно. Значит, одно из конических сечений имеет самое тесное отношение к прогрессиям. Как все это связано!

— Вот эта связь различных разделов математики друг с другом и есть величайшая драгоценность нашей науки [27] Наш симпатичный читатель поступит дельно, если раздобудет себе небольшую книжечку «Задачи по элементарной математике», составленную группой преподавателей под руководством чл.-корр. АН СССР И. М. Гельфанда (М., «Наука», 1965). Вся эта серия брошюр («Библиотечка физико-математической школы») очень полезна для юного математика. .

— Как интересно! — воскликнул Илюша. — А скажи, пожалуйста, когда были открыты логарифмы?

— В начале семнадцатого века Джоном Непером, шотландцем.

— А-а! — сказал Илюша. — Вот в чем дело-то! Вот при чем тут шотландский сыр!

— Конечно! Про этого Непера говорили, что он увеличил вдвое продолжительность жизни астронома, потому что с логарифмами можно насчитать вдвое больше, чем без них. Разумеется, нетрудно догадаться, что все, что мы проделали с неделимыми, можно отлично перевести и на современный язык теории пределов, стоит только вместо суммы «неделимых полосок» рассматривать предел суммы бесконечно утончающихся вписанных или описанных прямоугольничков, как мы делали уже в Схолии Пятнадцатой.

— А теперь расскажи еще про гиперболу. Греки определили параболу как геометрическое место. А гиперболу нельзя так определить?

— Можно. И гиперболу и эллипс. В эллипсе есть две весьма замечательные точки. Чтобы показать их тебе, я впишу в конус два соприкасающихся шара: один поближе к вершине конуса, другой подальше. Второй шар будет побольше, первый поменьше. Теперь я просуну между ними секущую плоскость (которая, разумеется, не имеет толщины). Оба шара будут ее касаться в одной точке, если плоскость будет лежать параллельно основанию конуса. И эта точка касания будет центром той окружности, которая будет сечением конуса этой самой плоскостью. Теперь я начну секущую плоскость наклонять.