Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ
- Название:ВОЛШЕБНЫЙ ДВУРОГ
- Автор:
- Жанр:
- Издательство:Детская литература
- Год:1967
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ краткое содержание
«В этой книге в занимательной форме рассказывается немало интересного для тех, кто любит точные науки и математику. Читатель узнает о развитии математики с ее древнейших времен, о значении математики в технике, а особенно об одной из важнейших отраслей математики — так называемом математическом анализе. На доступных примерах читатель познакомится с элементами дифференциального и интегрального исчислений. В книге также говорится о неевклидовых геометриях и о той, которая связана с открытиями великого русского геометра П. П. Лобачевского. Читателю предлагается немало занимательных задач, многие из которых сопровождаются подробным разбором.
Для среднего и старшего возраста.»
Некоторые рисунки и значительная часть чертежей нарисованы заново с целю лучшей читаемости на портативных читалках. В силу этого возможны незначительные расхождения с оригиналом, особенно в использованных шрифтах, расположении и размере надписей на рисунках. Расположение некоторых рисунков по отношению к тексту также изменено. В электронной книге для оформления применяются стили, поэтому для чтения лучше использовать CR3. Таблицы приводятся в формате fb2 и дублируются либо в текстовом, либо в графическом варианте. В связи с многочисленными отсылками к номерам страниц сохранена нумерация печатного оригинала. Номер размещен в конце страницы. — V_E.
ВОЛШЕБНЫЙ ДВУРОГ - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
— Ну, а про магнитные и электрические поля я как-то слышал, что целый ряд задач из физики решается тоже таким путем?
— Конечно. Без того, что называется в математике анализом, то есть без дифференциалов и интегралов, вообще ни—
— 361 —
какой электротехнической культуры не было бы, а тем более таких чудес, как радио, телевидение и прочее.
— Так, — сказал Ильюша, — хорошо. А теперь ты расскажи мне немножко про логарифмы. Правда, мы скоро их будем проходить, но все-таки ты расскажи. И потом, какое же они имеют отношение к гиперболе?
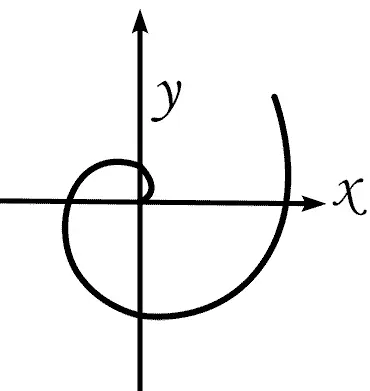
Спираль Архимеда, которая умеет делить угол на любое число
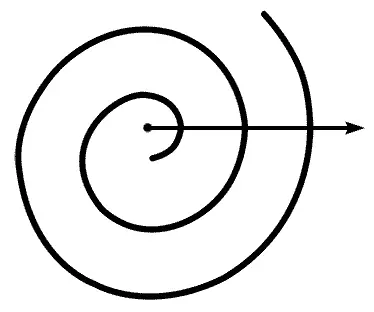
Декартова равноугольная спираль. Она может заменять умножение сложением
— Если взять две прогрессии и написать одну около другой — арифметическую и геометрическую, — то мы получим табличку, которая напечатана на странице 361 {13} 13 В электронной книге таблица перенесена и расположена ниже. — V_E.
.
| А | Г | А | Г |
|---|---|---|---|
| 1 | 2 | 11 | 2048 |
| 2 | 4 | 12 | 4096 |
| 3 | 8 | 13 | 8192 |
| 4 | 16 | 14 | 16384 |
| 5 | 32 | 15 | 32768 |
| 6 | 64 | 16 | 65536 |
| 7 | 128 | 17 | 131072 |
| 8 | 256 | 18 | 262144 |
| 9 | 512 | 19 | 524288 |
| 10 | 1024 | 20 | 1048576 |
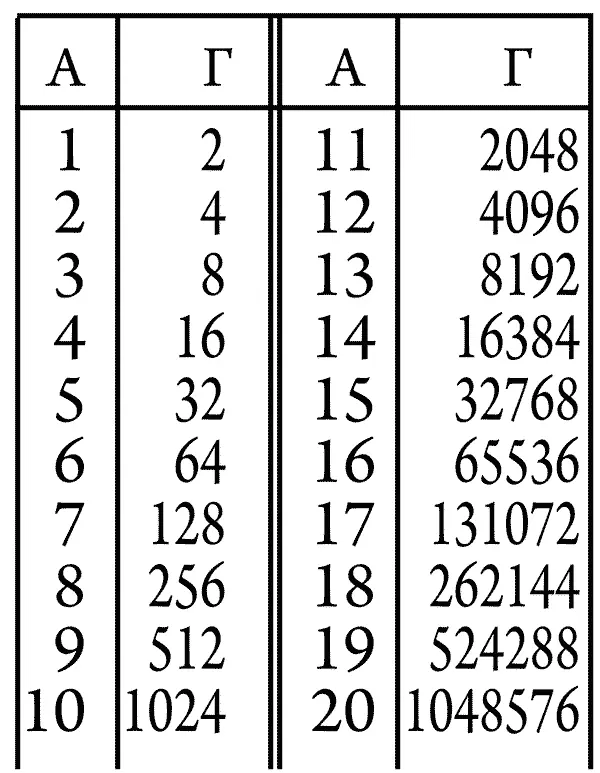
Второй столбец (под буквой «Г») — это ряд степеней числа «два». А первый (под буквой «А») дает самые степени. Не правда ли?
— Конечно, — отвечал мальчик. — Два в четвертой степени будет шестнадцать, а в пятой — тридцать два. Понятно!
— Так вот, допустим, что надо умножить четыре на шестнадцать. По правилу сложения степеней, так как четыре — это два в квадрате, а шестнадцать — это два в четвертой степени, просто можно сложить эти показатели. Складывая два и четыре получаем шесть, а два в шестой степени есть шестьдесят четыре. Так как есть таблица, то нет необходимости вычислять, чему равно два в шестой степени, а просто надо найти то число, которое стоит во втором столбце рядом с цифрой «шесть» из первого столбца. Следовательно, теперь можно вместо умножения складывать. Ты находишь во втором столбце свои множители. Потом выписываешь соответственные им числа из первого столбца, складываешь их, а получив сумму, смотришь, какое число во втором столбце соответствует этой сумме. Ну-ка, попробуй сам!
— 362 —
— Сейчас, — сказал Илюша. — Я буду множить 2048 на шестнадцать. Двум тысячам сорока восьми соответствует и первом столбце одиннадцать, шестнадцати соответствует в первом столбце четыре. Надо, следовательно, сложить одиннадцать и четыре. Получаю пятнадцать. Ищу пятнадцать в первом столбце, а рядом нахожу во втором столбце ответ — 32768. Проверяю умножением… Совершенно верно!
— Ну вот это и есть принцип логарифмов. Сложение заменяет умножение, вычитание заменяет деление…
— А! Как со степенями! — воскликнул Илюша. — Значит, чтобы возвести в степень, надо умножить, а чтобы извлечь корень — разделить. Я попробую! Во-первых, деление. Например, нужно разделить 524288 на 4096. Значит, я должен вычесть из девятнадцати двенадцать. Получается семь, то есть выходит в результате деления сто двадцать восемь. Ну-ка, попробуем на бумажке. Так и есть! Теперь, во-вторых, я хочу возвести шестьдесят четыре в квадрат. Значит, надо шесть умножить на два. Получаю двенадцать, окончательный результат по таблице — 4096. Проверим!.. Точно! Теперь, в-третьих, из 65 536 я извлекаю квадратный корень. Значит, придется шестнадцать разделить на два. Получаю восемь. Выходит двести пятьдесят шесть. Ну-ка, я проверю!
Повозившись немного, Илюша извлек корень и сказал:
— Да, вот уж с корнем-то ясно, какая получается значительная экономия времени! А тут разделил на два — и все. А если надо кубический корень извлечь? С кубическим совсем заплачешь… Впрочем, постой-ка! Ведь с этой табличкой можно, наверно, и кубический корень попробовать извлечь. Если я возьму, например, число 262144 и извлеку из него кубический корень?.. Значит, нужно восемнадцать разделить на три. Получаю шесть. А шести соответствует число шестьдесят четыре. Проверим! Шестьдесят четыре в квадрате, как я уже выяснил, равняется 4096. Ну, а если я умножу это число еще раз на шестьдесят четыре?.. Совершенно верно. Ведь так можно, пожалуй, и четвертой степени корень извлечь? Правильно? Извлекаю корень четвертой степени из числа 1 048 576… и получаю тридцать два. А ну-ка, проверим! Тридцать два в квадрате будет 1024, а 1 024 в квадрате — 1048576. Да это замечательный способ! А что такое основание логарифмов?
— В нашей табличке основанием будет два. Это то число, степень которого ты видишь во втором столбце. Общий принцип сопоставления двух прогрессий, арифметической и геометрической, был известен еще Архимеду. Это, конечно, не значит, что Архимед представлял себе смысл логарифмов, но для математиков нового времени его замечания могли иметь известное значение.
— 363 —
— Теперь я понимаю, что значит эта фраза: «Логарифм какого-нибудь числа есть показатель степени, в которую надо возвести основание, чтобы получить это число». В нашей табличке основание есть двойка, первый столбец — это логарифмы, а второй — числа. Ну, а чем же отличаются настоящие таблицы логарифмов от этой?
— Только тем, что у них основание не два, а десять.
— Так это очень просто! — вскричал Илюша.
— Несложно, если не считать того, что во втором столбце стоят не только точные степени десяти, но и все промежуточные числа, — отвечал Радикс. — А записываем мы это так:
log 232 = 5,
то есть: «Логарифм тридцати двух при основании два равен пяти». А при основании десять тот же самый логарифм будет равен:
1,50514997831990597607,
с точностью до девятнадцатой цифры после запятой.
— А можно перейти от одного основания к другому? — спросил Илюша.
— Это нетрудно, — отвечал Радикс. — Если ты разделишь двоичный логарифм на десятичный логарифм, то получишь так называемый модуль перехода, с помощью умножения на который из любого десятичного логарифма получишь двоичный. В данном случае этот модуль будет примерно равен 3,3219. Вывести общее правило для получения модуля перехода тоже дело нехитрое. Раз ты умеешь из старого основания а получать любое число, то задача, очевидно, сводится к тому, чтобы из нового основания b получить старое основание а .
Читать дальшеИнтервал:
Закладка:










