Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— 351 —

Видно, что сумма прямоугольников больше, нежели сумма трапецоидов, но при безграничном увеличении числа n искомая площадь будет пределом суммы прямоугольничков, то есть пределом следующего выражения:

h ( h 2+ 2 2 h 2+ 3 2 h 2+ … + n 2 h 2) = h 3(1 2+ 1 2+ 2 2+ 3 2+ … + n 2) = b 3/ n 3(1 2+ 1 2+ 2 2+ 3 2+ … + n 2)

А так как шахматная доска уже объяснила нам, что сумма первых и квадратов натурального ряда равна

(2 n + 1)( n +1) n / 6

то мы, подставляя это выражение в предыдущую формулу, после некоторых несложных переделок получим:

b 3/6 (1 + 1/ n )(2 + 1/ n )

Спрашивается: что будет с этим выражением, если число n будет неограниченно возрастать? Ясно, что дробь 1/ n будет неограниченно приближаться к нулю и ею мы можем пренебречь. В таком случае предыдущее выражение в пределе обратится в

b 3/3

что и является результатом нашего интегрирования. Знай, что это один из первых интегралов, полученных человеком, что человека этого звали Архимед и что он рассуждал примерно так, как и мы.

И тут Величайший Змий вырос снова перед ними. Он взглянул на Илюшу, и мальчику показалось, что это могущественное чудовище даже улыбнулось!

— 352 —

в которой Илюша припоминает разные разности из предыдущих схолий, оставшиеся не совсем ясными, а Радикс рассказывает ему об истории надгробного камня Архимеда, погибшего от меча римского грабителя, о спирали Архимеда. Затем следует масса любопытнейших подробностей о веретенах, о шотландском сыре, о фокусах, которые придумали древнегреческие геометры, о том, как в старину индусы решали кубические уравнения, как в шестнадцатом веке бедный мальчик-заика учился на кладбище грамоте, а также почему у квадрата такая большая площадь и что по этому поводу думает касательная; о битве за высоту над городом Клермоном. А затем Илюша присутствует при волшебном опыте, который поясняет, что такое прямая линия и какие чудеса с ней случаются при ее путешествиях в мировом пространстве. Вслед за этим Илюша и Радикс видят нечто чрезвычайно странное… Но пока это еще страшный секрет, который, может быть, раскроется в будущем…

— Ну, теперь ты доволен? — спросил Радикс.

— Да, — сказал Илюша, — я узнал массу интересных вещей. Теперь я, кажется, понимаю, почему так уважают Архимеда и как велико могущество Змия. Но только у меня есть еще вопросы.

— Ну что ж! Давай твои вопросы. Может быть, как-нибудь вдвоем разберемся.

— 353 —

— Помнишь, ты где-то, кажется в Схолии Одиннадцатой, перечислял мне титулы Величайшего Змия? Так вот, я хотел тебя спросить о них. О площадях я теперь понял: путем интегрирования можно получить площадь любой криволинейной фигуры. С объемами я тоже как будто сообразил. Это, вероятно, делается путем суммирования бесконечно тонких слоев тела, как Демокрит считал объем конуса?

— Правильно. А сейчас мы можем закончить вывод формулы для объема конуса, о которой мы толковали в Схолии Пятнадцатой. Если рассечь конус плоскостью, проходящей через его ось, то получится треугольник. Из рассмотрения этого треугольника ты убедишься в том, что радиус основания цилиндрика, отстоящего на расстояние h от вершины, определится при помощи пропорции:

r / R = h / H

где R — радиус основания, а H — высота конуса. Отсюда

r = ( R / H ) h

и площадь основания цилиндрика будет

πr 2= π ( R 2/ H 2) · h 2

Теперь предположим, что мы делим высоту конуса на n частей. Тогда высота каждого цилиндрика будет H / n , а последовательные расстояния оснований цилиндриков от вершины конуса, то есть радиусы этих оснований, будут

h , 2 h , 3 h ,… nh .

Поэтому сумма объемов этих цилиндриков равна

π ( R 2/ H 2) · H / h ( h 2+ 2 2 h 2+ … + n 2 h 2) = π R 2/ H (1 2+ 2 2+ … + n 2) / n 3

Как и в предыдущей схолии, ты убедишься, что предел последнего множителя при неограниченном возрастании n будет равен ⅓, и для объема конуса получается выражение:

⅓ πR 2 H

— 354 —

Множитель ⅓ ты можешь рассматривать как лежащую на этой формуле печать Великого Змия.

— Как интересно! — сказал Илюша. — А с объемом шара можно справиться таким способом?

— Я приведу тебе только чертеж, который, по преданию, Архимед завещал вырезать на своем надгробном памятнике.

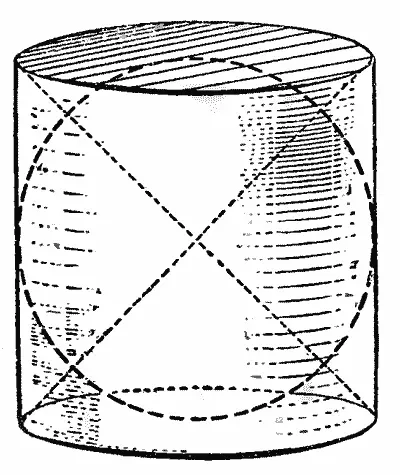
Здесь ты видишь цилиндр, вписанный в него шар радиуса R и конус. Разбей все три тела на тонкие «цилиндрические» слои и легко установишь, что на расстоянии h от центра шара площадь поперечного сечения самого шара равна:

π ( R 2— h 2) = πR 2— πh 2

то есть разности площадей поперечных сечений цилиндра и конуса. Суммируя объемы всех тонких цилиндрических пластинок и переходя к пределу, как мы это делали для конуса, находим, что и объем шара тоже будет равен разности объемов цилиндра и конуса. Этот закон и был открыт Архимедом. Таким путем можно найти не только объем всего шара, но и объем любого шарового слоя. В формулы войдет опять множитель ⅓, печать Великого Змия, свидетельствующая о том, что здесь приходилось интегрировать функцию, содержащую квадрат переменной (в данном случае — квадрат высоты h ).

— Очень хорошо! — отвечал мальчик. — А теперь вот еще что. Ты назвал Великого Змия развертывателем спиралей. Что это значит?

— Это значит, что путем интегрирования можно получить длину дуги любой кривой, например параболы, окружности и так далее. В частности, и длину спирали. Мы ведь уже говорили, как находится длина дуги.

— Но я должен сознаться, — вздохнув, сказал Илюша, — что до сих пор не пойму, как при помощи этой спирали получается длина окружности, то есть почти квадратура круга?