Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— Это можно, — сказал Радикс. — Ну, выкладывай, чего ты не понял.

— Во-первых, — начал Илюша, — часы…

В это время какие-то часы звучно пробили четыре. Илюша обернулся и увидел странный циферблат.

— Что такое? Бьют четыре, а показывают десять!

Илюша внимательно поглядел на часы. Раз-два-три… десять?.. Снова — раз-два-три и опять новый десяток?

— Ох! — воскликнул Илюша, хлопнув себя по лбу. — Другой циферблат! Да это не десяток! Чепуха какая! Это просто другая система исчисления. Четверичная система. Первый класс — единицы, потом второй — четверки… а следующий класс будет четыре в квадрате, то есть шестнадцать. Как у нас на первом месте единицы, на втором — десятки, а третье место занимают сотни, а это ведь десять в квадрате. У нас число пишется так:

a 10 0+ b 10 1+ c 10 2+ …,

а у них:

a 14 0+ b 14 1+ c 14 2+ …,

причем а , b , с … могут принимать все значения от нуля до девяти, но a 1, b 1 c 1 … могут принимать значения от нуля до трех. И так далее. Если, значит,

— 55 —

написать девятнадцать по этой системе, будет шестнадцать плюс три, то есть сто три. А если взять сто, то выйдет тысяча двести десять. Экая досада, что я не догадался!

— Штука нехитрая, — сказал Радикс.

— Вот то-то и обидно! — отвечал Илюша.

— Они тебя, — заметил Радикс, — все-таки немножко надули. То есть были приняты меры к тому, чтобы ты не догадался. Ведь перерыв-то у них сдвинут так, что прием кончается раньше перерыва.

— Экая досада! — возмущенно повторил Илюша. — А все-таки я должен был догадаться!

— Разумеется. Зевать не надо. Ну-с, далее?

— Дальше вот что. Часы что — это пустяк, шутка…

— Не всегда, — заметил Радикс, посмеиваясь.

— Ну все-таки. А вот этот невсис… Я о нем даже не слыхал. Прямо удивительно. Поставь на линейке две метки — в сразу готово!

— В том-то вся и сила, что просто. Узнаешь немного погодя.

— А потом все эти мои скитания по коридорам. Ведь это был настоящий лабиринт. Так или нет?

— Не совсем настоящий, но вроде этого.

— Я решил, что если все время буду держаться правой или левой рукой (это все равно, только не менять руку) за стену, то можно дойти до середины и выйти назад.

— Почему ты так решил?

Илюша постарался изложить своему другу все, что придумал о сходстве лабиринта с тупиком.

Радикс выслушал и процедил:

— Да-а… Но я берусь выстроить лабиринт, где твое правило правой руки ни к чему не приведет. В лабиринт надо войти, дойти до некоторой заранее определенной точки, которая будет центром этого лабиринта, и выйти обратно. Не так ли?

Илюша согласился.

— Так вот. Мой лабиринт будет представлять собой то, что ты называешь петлей. То есть тот же тупик, только вместо замыкающей стенки будет еще один кругообразный ход. В середине этого хода находится островок, в нем дверь, за ней коридор, который и кончается той точкой — центром. Далее я утверждаю, что какой бы рукой ты ни пользовался, правой или левой, ты обойдешь мой лабиринт, выйдешь обратно, но не попадешь в центр, и задача не будет решена. Что ты на это скажешь?

Илюша нарисовал чертеж и углубился в его рассмотрение.

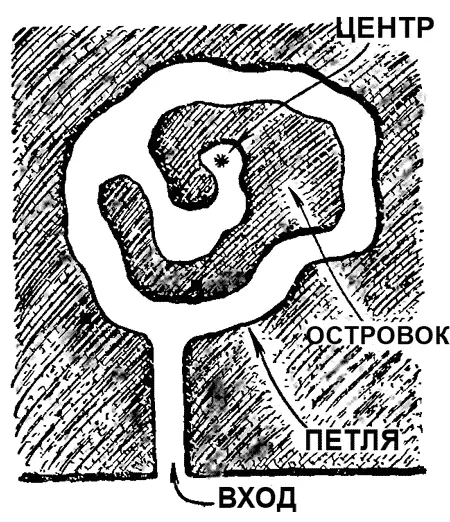
Двойной лабиринт Радикса.

— Да, — сказал Илюша, — действительно, в центр не по-

— 56 —

паду. Тогда, мне кажется, можно поступить так. При обходе лабиринта по правилу правой руки я убеждаюсь, что в центр не могу попасть, и замечаю, что какой бы рукой я ни пользовался, всегда на противоположной от меня стене, то есть на той, которой я не касаюсь рукой, мне встречается дверь, и я в нее не попадаю. Если в лабиринте есть такая дверь, то я поставлю против нее крестик на моей стене, сменю руку и пойду кругом островка. Когда я попаду в эту дверь, то дойду до центра, выйду из него и, снова дойдя до моего крестика, сменю руку во второй раз. Мне кажется, что это получается лабиринт в лабиринте, и, по-моему, такой лабиринт надо называть двойным. Так можно и тройной построить!

— Можно, — спокойно ответствовал Радикс. — Во-первых, эта система внутренних петель и островков может быть довольно сложной, а во-вторых, именно на такого рода усложнениях и основана путаница лабиринта. Ну, что у тебя еще есть? Выкладывай. А к лабиринту мы вернемся еще.

— Еще про этого противного Доктора Узлов. Почему он так называется?

— Начнем с его рожицы, — отвечал Радикс. — Ее линии, как ты заметил, легко можно обойти, пройдя при этом один раз по каждой линии. Такая фигура называется уникурсальной . Вот почему его так зовут.

Правда, это слово — «уникурсальный» — иногда применяется и в другом смысле, но уж этого мы касаться не будем. Уникурсальную фигуру можно начертить, не отнимая пера от бумаги, как говорится — одним росчерком. Конечно, так начертить можно не всякую фигуру. Попробуй, например, начертить фигуру, нарисованную налево.

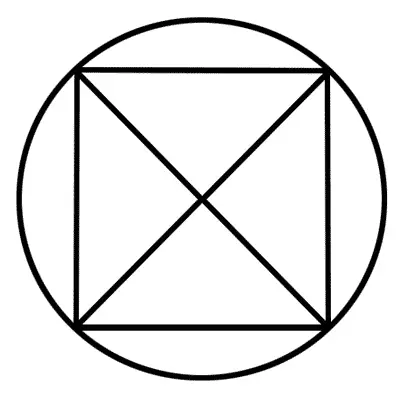
Попробуй начертить одним росчерком!

У тебя ничего не получится, как бы ты ни старался. Эта фигура не уникурсальная.

— В чем же тут дело? — спросил

— 57 —

Илюша. — Как узнать, какая фигура уникурсальная, а какая нет?

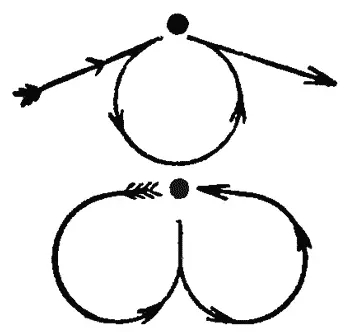
Четный узел

— Назовем каждый перекресток нашей фигуры узлом. Если от него отходит четное число путей, то это будет четный узел, а если нечетное — нечетный. Если узел четный, то ты можешь прийти к нему и уйти от него по новому пути. Сколько бы ни было четных узлов, они тебе не помешают.

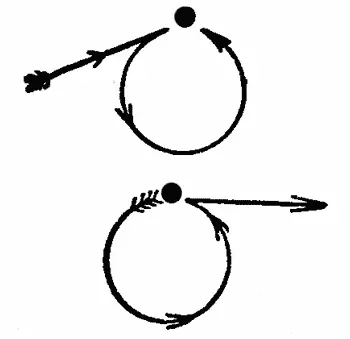
Нечетный узел.

В каждый из них ты можешь пройти. Другое дело — нечетный узел. Например, из него три пути…

— Ясно, — подхватил Илюша. — Раз приду и раз уйду — значит, две дороги я уже использовал. А опять приду по третьей — и конец, потому что нехоженых дорог больше нет.

— Совершенно верно, — отвечал терпеливый Радикс. — Ну, а что будет, если ты встретишь два нечетных узла?

— Допустим, что они будут тройные.

— Два нечетных узла?.. — повторил Илюша. — Я сейчас нарисую.

Илюша нарисовал два чертежа.

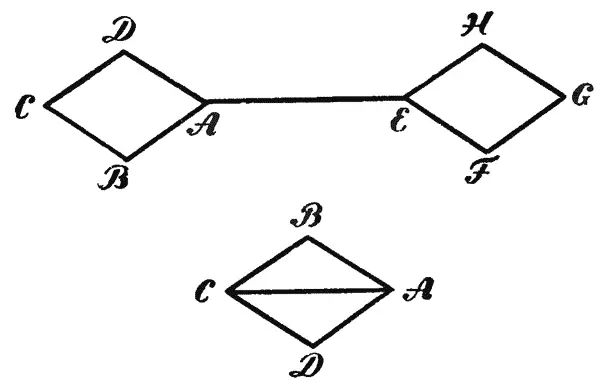
Один изображал два ромба, соединенных прямой, а другой ромб с одной диагональю (рисунок на стр. 59).