Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

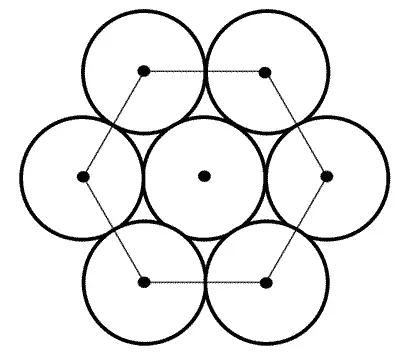
— Но это еще не все, — добавил Радикс. — Дело в том, что наиплотнейшее расположение шаров в пространстве, даже в три только слоя, зависит от того, в какие лунки ты кладешь ядра и какие ты пропускаешь. Чтобы это стало совершенно ясным, составим тетраэдры в два слоя так, чтобы соприкасающиеся углы их совпали, и допустим, что эти два слоя тянутся безгранично далеко. У каждого из тетраэдров есть вершина, которая изображает в нашей схеме шар второго слоя. Теперь я хочу добавить еще третий слой, но добавить его не сверху, а снизу. И при этом я могу действовать двумя способами. Либо я к каждому основанию моего тетраэдра приклею основание еще одного (чтобы они совпали и слились воедино), и тогда вершина второго тетраэдра будет стоять симметрично относительно вершины первого. Это первый способ наиплотнейшего расположения шаров в

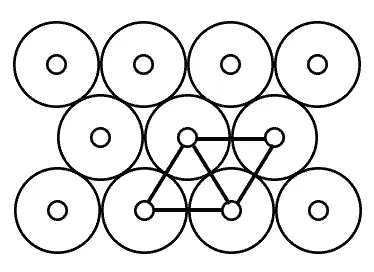
Наиболее плотное расположение кругов на плоскости.

— 122 —

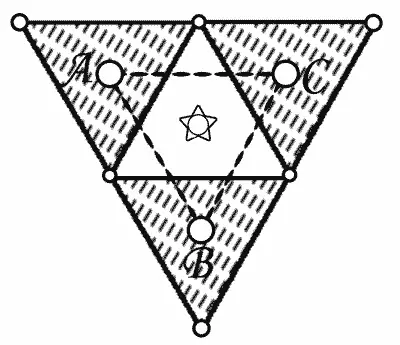
Четыре тетраэдра (план). Заштрихованные треугольники — основания трех нижних тетраэдров; кружки — вершины этих тетраэдров ( А , В , С ); звездочка — положение верхнего шара, то есть вершины четвертого тетраэдра, основание которого совпадает с пунктирным треугольником ABC .

пространстве. Однако можно действовать и по-другому, то есть приложить основание второго тетраэдра к той впадине, которая образуется между двумя рядом стоящими тетраэдрами. Тогда третий, нижний слой шаров будет расположен так, что его можно перевести в первый при помощи того же смещения, которое переводит первый ряд во второй. Комбинируя эти два основных способа укладки, можно получить различные расположения шаров в пространстве. Так вот, куча из ядер, о которой мы с тобой сейчас толкуем, построена по…

— Второму способу! — закончил Илюша. — Ну, теперь ясно, что на Арамиса должны нападать трое сверху, трое снизу и шесть человек со всех сторон! Выходит не так, как всегда говорят: «со всех четырех сторон», а со всех двенадцати сторон! Интересно, сколько же в куче будет всего ядер? Наверху — одно, в следующем слое — столько, сколько видно сбоку в первом треугольнике, то есть три, а в следующем — столько, сколько во втором треугольнике; это будет еще на три ядра больше, значит, шесть. Потом будет уже на четыре больше — десять. Как же считать?

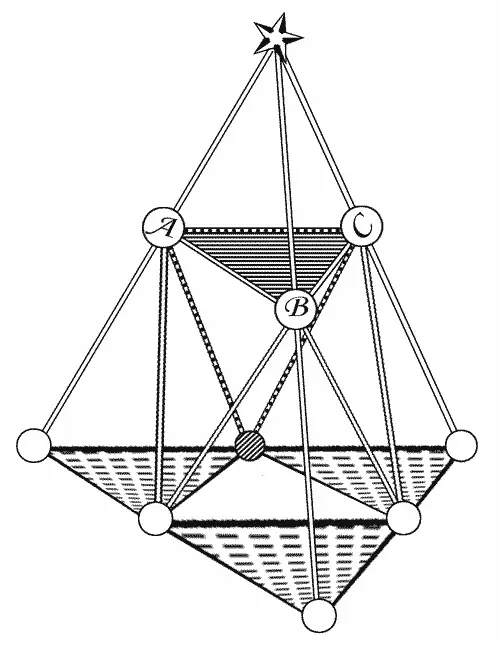
Четыре тетраэдра (вид сбоку).

— Об этом ты узнаешь в Схолии Одиннадцатой, а пока продолжай складывать.

— В первом и втором слоях вместе: один да три — четыре.

— Квадрат двух, — подсказал Радикс. — А во втором и третьем?

— Три и шесть — девять,

— 123 —

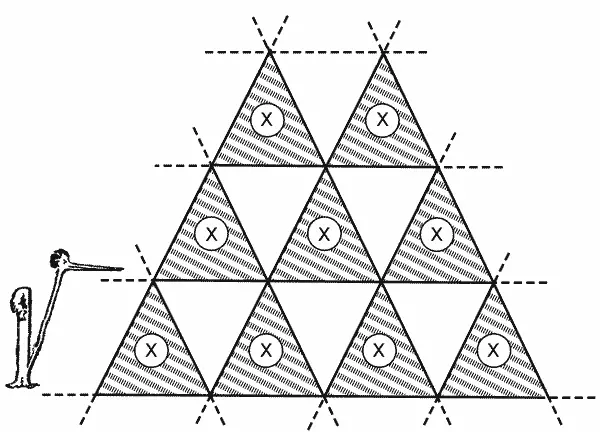
Первый способ наиплотнейшего расположения шаров. Шары верхнего слон (кружки) закрывают шары нижнего слоя (крестики).

опять квадрат. А шесть и десять-шестнадцать, опять квадрат.

— Три и шесть — девять, опять квадрат. А шесть и десять — шестнадцать, опять квадрат. Как интересно! Значит, очень просто эти слои считать: вычти число последнего слоя из следующего квадрата и получишь то, что надо. Следующий квадрат будет двадцать пять. Вычитаю десять, и выходит пятнадцать. Так?

— Твое наблюдение правильно. Это треугольные числа.

— Как интересно! — воскликнул Илюша. — И для всякого числа есть свое название! А выходит, что шесть — это очень знатное число: оно и совершенное и треугольное! Теперь: сколько же всего ядер выходит в куче?

Один слой — одно. Два слоя — четыре. Три слоя — десять. Четыре слоя — двадцать. Пять слоев — тридцать пять.

Строение селитры по М.В. Ломоносову (1763 г.)

— А это пирамидальные числа.

— Ну да, потому что выходит пирамида из ядер.

— Конечно, — сказал Радикс. — Такое расположение имеет важное значение при изучении места отдельных

— 124 —

атомов или молекул в кристаллах. Они там тоже так уложены. Представь себе, что математики пришли к этой мысли раньше, чем физики! И все эти числа получить очень просто. Возьми-ка мел и пиши. В первом столбике напиши одну под другой пять единиц; во втором — те числа, которые ты видишь в пирамиде ядер сбоку; в третьем столбике — треугольные числа, а в четвертом — пирамидальные.

Илюша взял мел и написал то, что изображено справа.

— Смотри, какая у тебя получилась табличка. Каждое число в любой строке равно сумме того числа, которое стоит над ним, и того, которое стоит слева от него. Видишь?

— Верно, — отвечал Илюша. — Например, десять равно шести плюс четыре!

— А теперь, — продолжал его друг, — ты видишь, что эту табличку очень легко продолжить по этому правилу. Добавь-ка еще четыре единички в первой строке и три в первом столбце и заполни таблицу. И в каждой строке пиши одним числом меньше, чем в верхней. Ну-ка, пиши поскорей!

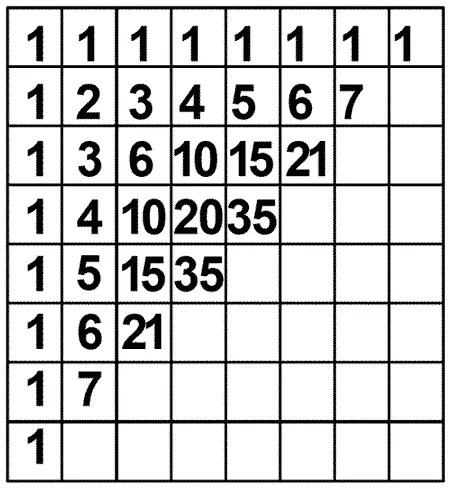Илюша написал единицы, и у него получилась табличка, изображенная слева.

— Эта замечательная табличка называется треугольником Паскаля, — сказал Радикс, — потому что она была составлена французским математиком семнадцатого века Блезом Паскалем.

— Это тот самый, про которого ты вспоминал, когда Великий Змий пришел пробирать нас? — спросил Илюша.

— Он самый, — торжественно произнес Радикс. — Эту табличку до Паскаля, веком раньше, построили итальянские математики. Но в то время известия о новых открытиях распространялись не так быстро, как теперь. Мало того, что этот треугольник дает натуральные числа, треугольные, пирами-

— 125 —

дальние и многие другие, которые в общем называются фигурными числами, он дает еще более полезные и важные указания. Вот я его сейчас перепишу по-другому.

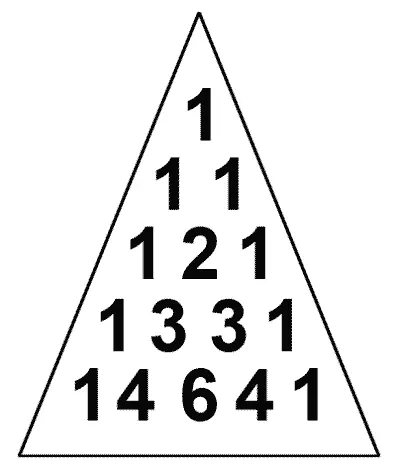Радикс взял мел и написал то, что изображено слева.

— Посмотри, — сказал он. — Тебе эти цифры ничего не напоминают?

Илюша внимательно посмотрел новую табличку, подумал, потом сказал:

— Один, два, один — это похоже на сто двадцать один, то есть на квадрат одиннадцати.