Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— Сей аппарат, — грустной скороговоркой, как заученный наизусть урок, забормотал Коникос, — есть наша неутомимая Центрифуга. В высшей степени полезное изобретение сие представляет собой механический станочек для получения поверхностей вращения. Так-с… Начнем с начала, как в таких случаях и полагается. Знаешь ли ты, дружок, как делается конус?

Асимптотос приволок откуда-то огромный прямоугольный треугольник, прикрепил его большой катет к стержню Центрифуги и подобострастно сказал станочку:

— Будьте добры, матушка-кормилица, не откажите!

Стержень Центрифуги начал вращаться, и при этом все скорее и скорее. Вместе с ним вращался и прямоугольный треугольник, пока наконец быстро мчащаяся по кругу гипотенуза треугольника не обратилась в серенький туман, действительно напоминавший конус. Тут Асимптотос подмигнул Центрифуге, и аппарат немедленно остановился. А конус остался стоять. В этом, по всей видимости, и заключалось волшебство. Тут Асимптотос поднял конус и поставил его на пол. Конус был красивый, отменно тонкий, внутри пустой, и высота его была два метра.

Коникос принес громадный, широченный нож, нерешительно посмотрел на собравшихся и сказал, опасливо покосившись в ту сторону, где исчез доктор Уникурсальян:

— 240 —

— Это у нас будет как бы секущая плоскость.

Тут Коникос стал на табуретку и срезал самую верхушку конуса, причем его широкий нож двигался в точности параллельно основанию конуса.

Затем он показал Илюше, что получилось на месте среза, и спросил:

— Круг?

— Круг, — отвечал Илюша.

И тут мальчик вспомнил, что ему как будто не зря толковал громкоговоритель про голландский сыр. Так как доктор Уникурсальян У. У. запретил поминать о сыре, то он молча поглядел на Асимптотоса, потом на Коникоса, потом на Радикса, потом на то самое место на полу, куда бесследно провалился конический сыр. Тогда Коникос знаками пояснил ему, что голландский сыр обычно имеет форму шара и, значит, как его ни режь, в сечении обязательно получится круг — фигура, которая у древних мудрецов символизировала нечто совершенное.

— Теперь, — сказал, Асимптотос, — следующий разрез. Тоже предмет, достойный внимания!

И он начал резать конус, который уже опять был целый, поставив свой широченный нож параллельно образующей конуса. Затем он поднес Илюше отрезанный кусок. Теперь срез имел форму дуги и показался Илюше знакомым.

С большой опаской и поминутно оглядываясь туда, где расплылся и исчез свирепый и неумолимый Доктор Четных и Нечетных, Асимптотос при помощи мимики и жестов дал понять Илюше, что именно об этом-то срезе — то есть об этом-то сечении конуса! — ему и говорила лесная девица Дриада, поминая какую-то «Радость Кита». Когда же Илюша шепотом спросил его, при чем же здесь, собственно, сыр, Асимптотос, весь дрожа от страха, снова знаками пояснил ему, что если бы У. У. Уникурсальян, К. T. Н., Д. Ч. и Н. У. и проч., не был таким сердитым, то они бы ему показали, что их сыр (тот, который провалился) менял свой дивный вкус в зависимости

— 241 —

от того, как его резали, и что, разрезанный параллельно образующей, он и есть «Радость Кита», которая смертельна для врагов. Не успел Илюша спросить, при чем тут враги и киты, как Радикс уже состроил кислую мину и сказал:

— Слушай! Ну… не надо. Ну, зачем так делать? Ведь нехорошо!..

Асимптотос густо покраснел и подал кусок конуса Илюше.

Как только Илюша взял в руки этот кусок, откуда-то раздался громкий треск и в воздух полетели сотни разноцветных ракет.

— Это в честь нашего сечения! — сказал Асимптотос. — Как ты видишь, ракеты летят в воздух по кривым, которые очень похожи на форму нашего среза. Когда снаряд летит из пушки, то он тоже двигается по этой кривой. Вот почему наш сыр так страшен врагам. Когда бьет фонтан, его струя летит вверх и падает так же, как ракета. Вот почему этот сыр так любят киты — это ведь они выдумали фонтан! Когда твои современники строят прожектор, то его отражательное зеркало тоже делается по этой кривой.

— Я ее где-то недавно видел! -воскликнул Илюша.

— Все может быть, — отвечал Коникос. — Может быть, ты видел большой бетонный железнодорожный мост? Может быть, ты видел кривую квадратов натурального ряда? Может быть, ты видел, как льется вода из бочки?

— Не-ет, — сказал Илюша. — Постой-ка! Радикс! А вот та кривая, которую мы рисовали в Схолии Двенадцатой?

— 242 —

— Мы их много рисовали…

— Вот та, которая получается из квадратного уравнения.

— Ах, эта! — воскликнул Асимптотос. — Она самая! Она называется параболой.

Однако Илюша успел уже сообразить, что сыр (тот самый, запрещенный, который провалился!), будучи параболически разрезан, приобретал особый, необыкновенный вкус и об этом-то и вспоминал милый Асимптотос.

— Итак, — продолжал Асимптотос, — срез помер третий! Внимание!

Теперь, когда Илюша взглянул на конус, то он увидел, что тот удвоился. Из вершины конуса вырос на той же самой оси еще один конус, стоящий вверх дном. Асимптотос снова начал резать. Теперь широкое лезвие ножа двигалось сверху вниз параллельно высоте нижнего конуса, то есть общей оси двух конусов. Как и следовало ожидать, Асимптотос отрезал сразу два кусочка от конусов.

— Необычайной формы! — заявил Асимптотос. — Идет главным образом на подтверждение закона Бойля-Мариотта, потому что объем газа обратно пропорционален давлению. В самом простом виде это сечение дает нам кривую обратных величин чисел. Если же эту кривую подвергнуть таинственной обработке [17] Об этом мы еще потолкуем в Схолии Семнадцатой. при помощи Знаменитого и Всемогущего Змия, то получается нечто совершенно неожиданное: продолжительность жизни астронома увеличивается ровно в два раза, так как новая кривая дает ему в руки логарифмы, а они очень сокращают длиннейшие астрономические вычисления. Кривая эта называется гиперболой. И если ты вспомнишь синьориту Одну Энную, то есть возьмешь за ординаты числа, обратные абсциссам, то эту кривую и получишь.

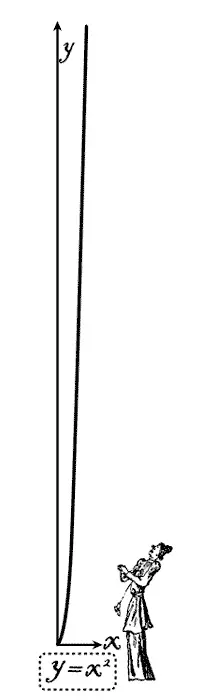
Кривая квадратов натурального ряда.