Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— Мы все друзья и слуги ВОЛШЕБНОГО ДВУРОГА! — отвечал Асимптотос, торжественно подняв ввысь палец.

— А когда вы вешаете эти кривые в воздухе, это тоже волшебство?

— Не совсем! Я прикрепляю гиперболу к стержню при помощи со мнимой оси. Ну, а так как она мнимая, то ее, разумеется, довольно плохо видно. Вот и все! Если мы рассекаем два конуса с общей вершиной, мы получаем две ветви гиперболы.

Они симметричны в двух направлениях. Во-первых, они симметричны относительно действительной, или вещественной, оси гиперболы, параллельной оси нашего конуса. А во-вторых, они симметричны относительно воображаемой линии, перпендикулярной к оси конуса. Эта линия называется мнимой осью гиперболы. Вот я ее и надел на стержень.

Затем Асимптотос пу-

— 270 —

стил в ход быстролетную Центрифугу. Вскоре из двух ветвей гиперболы образовалась поверхность вращения, средняя часть которой представляла собой кольцо с загибающимися краями.

— Это однополостный гиперболоид вращения.

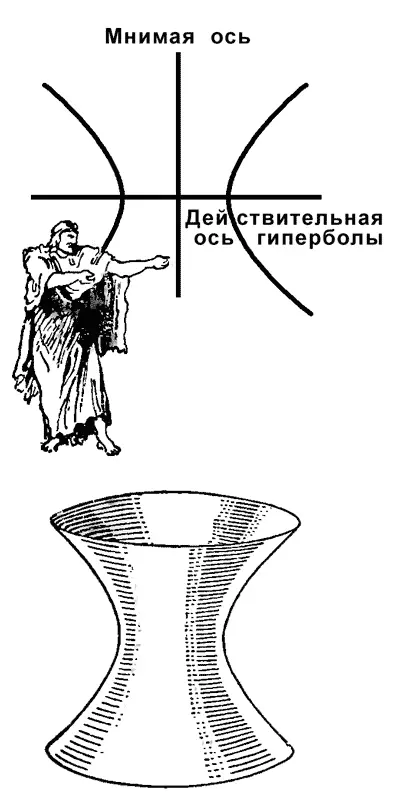
Однополостный гиперболоид вращения.

Если бы мы вращали гиперболу по вещественной оси, мы получили бы двуполостный гиперболоид, то есть две отдельные чаши. Ну, теперь все.

Он поставил гиперболоид на пол рядом с эллипсоидом.

— Начнем с эллипсоида. Замечаешь ли ты, что в длину он согнут не так, как в ширину? Ясно, что и в ширину он в сечении даст круг, но дело в том, что в длину, то есть по своей большой оси, если мы будем рассматривать точку над самой ее серединой, он гнется не так сильно, как гнется в том же месте по направлению малой оси.

— Конечно! — отвечал Илюша.

— Следовательно, в одном направлении у него одна кривизна, в другом — другая. Теперь я разрежу эллипсоид пополам и возьму два круга — один побольше, другой поменьше.

Асимптотос разрезал эллипсоид вдоль. Оказалось, что он внутри совершенно пустой. Получилось такое эллиптическое корытце, вроде половинки скорлупы фисташкового ореха, если бы, конечно, орех был в точности симметричен.

— Смотри! — сказал Коникос. — Маленький круг я могу в него вставить и по направлению малой оси и по направлению большой. Маленький круг совпадает с сечением эллипсоида по малой оси и измеряет его кривизну в этом направлении.

А большой круг по малой оси в это эллиптическое корытце не влезает, но зато он очень хорошо входит в корытце по большой оси. Конечно, круг не совпадает с сечением по большой оси, ибо это сечение есть эллипс, а не круг, но он соприкасается с этим сечением как только возможно тесно. Этот круг измеряет кривизну эллипсоида по большой оси, однако только в данной точке. Ясно, что круги становятся друг к другу перпендикулярно, потому что ведь и сами оси перпендикулярны.

Самое важное в этом случае то, что центры обоих кругов находятся с одной и той же вогнутой стороны эллипсоида. Понял? Вот когда центры кругов, измеряющих кривизну, оказываются с одной стороны поверхности, то такая кривизна

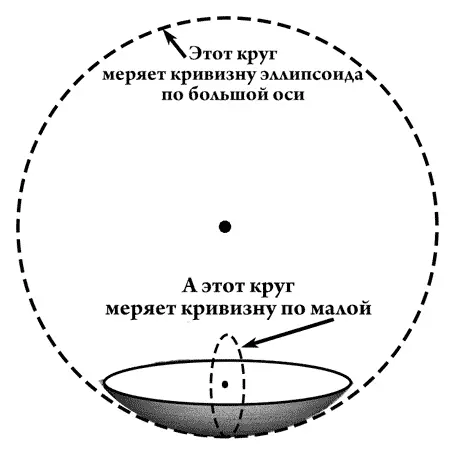
Центры кругов кривизны находятся по одну сторону поверхности — положительная кривизна.

— 271 —

называется положительной.

Откуда идут эти названия, сразу не расскажешь, и на этих тонкостях я останавливаться не буду. А теперь перейдем к гиперболоиду.

Асимптотос разрезал и гиперболоид вдоль.

Получились две седлообразные поверхности, похожие на горный перевал.

— Смотри внимательно! — сказал Асимптотос. — Я беру снова среднюю точку и буду измерять кривизну опять теми же кругами и по таким же двум взаимно перпендикулярным осям.

Когда Асимптотос начал приставлять круги к этой седлообразной поверхности, то оказалось, что эта поверхность в продольном направлении вогнутая, а в поперечном — выпуклая.

Поэтому центр большого круга оказался вне гиперболоида, а центр маленького — по другую сторону поверхности гиперболоида. Центры кругов оказались с разных сторон поверхности.

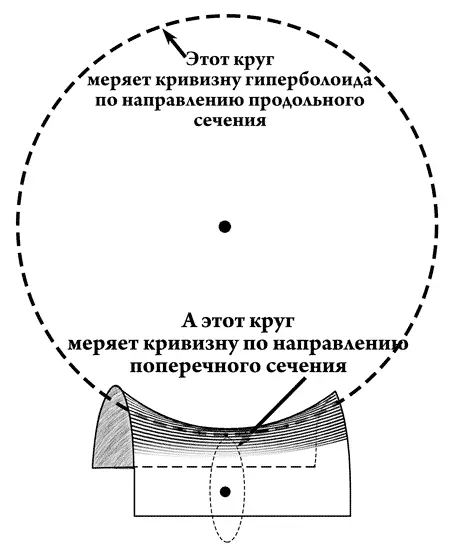
Центры кругов кривизны находятся с разных сторон поверхности — отрицательная кривизна.

— Ну вот! — сказал Асимптотос. — Когда центры кругов кривизны оказываются с разных сторон поверхности, то это и называется отрицательной кривизной. Геометрия Лобачевского осуществима только на поверхности с отрицательной кривизной. Однако слушай далее внимательно, ибо это еще не все. Сфера имеет во всех своих точках одну и ту же кривизну. Мы говорим, что эта поверхность постоянной положительной кривизны. Ясно, что хотя эллипсоид имеет тоже положительную кривизну, но она отнюдь не постоянна. Однополостный гиперболоид, наоборот, имеет отрицательную, но тоже непостоянную кривизну. Спрашивается: имеются ли поверхности постоянной отрицательной кривизны? Такие поверхности были открыты еще до Бельтрами. Отличительной особенностью поверхностей постоянной кривизны является то, что кусок такой поверхности может скользить по ней самой без разрывов и сжатий, как футляр шара по поверхности шара или кусочек бумаги по гладкой поверхности стола либо цилиндрической колонны. Важнейшее открытие Бельтрами состояло вот в чем: он обнаружил, что треугольники, сторонами которых являются кратчайшие линии на поверхности постоянной отрицательной кривизны, подчиняются «воображаемой» геометрии Лобачевского. Таким образом, выяснилось, что плоская геометрия Лобачевского осуществляется на одной из простейших поверхностей с постоянной отрицательной кривизной (именно такой поверхностью и является псевдосфера), и тогда уже не оста-

— 272 —

валось больше никаких сомнений в том, что в этой геометрии, как и в геометрии Евклида, нам нечего бояться противоречий.

— Ну, как Илюша? — сочувственно спросил Радикс. — Способен ли ты после этого соображать дальше или нет?

— Сейчас! — ответил Илюша. — Я только еще попробую.

Мальчик взял волшебно-математический аппаратик, измеряющий кривизну, и как только он приложил оловянный листик к поверхности гиперболоида, немедленно стрелка аппаратика пошла от буквы « Е» в другую сторону — это была самая настоящая отрицательная кривизна.

— Ясно? — спросил Коникос.

Илюша кивнул и сказал:

— Трудновато. Но мне кажется, я все-таки кое-что понял. А теперь я хочу наконец про Архимеда послушать!

— Ну что ж! — раздумчиво промолвил Коникос. — Теперь-то, пожалуй, уж можно… Да, постой-ка! Я вот еще что хотел тебе сказать, чтобы ты не забыл. Дело в том, что наш эллипсоид вращения можно еще сжать сверху вниз так, чтобы его круглое сечение тоже обратилось из круга в эллипс. И тогда из эллипсоида вращения получится трехосный эллипсоид, у которого все три оси но всем трем измерениям, то есть и в длину, и в ширину, и в вышину, разные или по крайней мере могут быть разные. Ясно, что как ни рассекай его по всем этим трем перпендикулярным направлениям, в сечении получишь эллипс. Например, кусочек туалетного мыла, который в просторечии нередко называют обмылочком, обычно как раз и имеет форму трехосного эллипсоида! Или морские камушки, обкатанные морскими волнами…