Сергей Бобров - ВОЛШЕБНЫЙ ДВУРОГ

— Как же так? — с удивлением спросил Илюша. — или это вроде этих сферических треугольников, не похожих на наши обыкновенные, плоскостные?

— Да, это в некотором смысле то же самое. На сфере тоже осуществляется не-евклидова геометрия, но это будет геометрия Римана, для которой, в отличие от геометрии Лобачевского, сумма углов треугольника больше двух прямых, а кроме того, там прямая линия безгранична, но не бесконечна…

— Что это значит? — спросил Илюша.

— Припомни, что такое экватор на глобусе. Ведь он границы не имеет, но он и не бесконечен. Не правда ли?

— Ах да, совершенно верно! — спохватился Илюша.

— Итак, — продолжал Радикс, — Бельтрами нашел такую поверхность, на которой «воображаемая» геометрия Лобачевского, по крайней мере в части планиметрической, осуществлялась, хотя и не совсем полностью. Эта поверхность напоминает стеклянную воронку и называется псевдосферой, или, если сказать более по-русски, это будет якобы сфера. Ее можно лег-

— 266 —

ко построить, и мы ее сейчас тебе покажем при помощи нашей Центрифуги. Таким образом Бельтрами, а за ним и многие другие ученые доказали, что «воображаемая» геометрия занимается вещами вполне реальными. Изучение и развитие неевклидовых геометрий оказало нашей науке громадные услуги, о которых ты, если будешь учиться дальше, узнаешь очень много. А если коснуться просто повседневной жизни, то и тут стоит сказать: то, что люди называли «естественной» геометрией, — это просто геометрия на плоскости. А когда землемер меряет поверхность горы или оврага, когда портниха шьет платье, то им нередко приходится иметь дело с «неестественными» геометриями, ибо оба они встречаются с седлообразными поверхностями, напоминающими ту же псевдосферу. Недаром замечательный русский математик Пафнутий Львович Чебышев занимался портняжьей проблемой кройки платьев и сделал в тысяча восемьсот семьдесят восьмом году доклад на эту тему в одном французском ученом обществе и даже представил при этом собравшимся его слушать ученым мяч, обтянутый двумя кусками материи в некотором, совершенно точном, смысле слова «наилучшим» образом.

— Вот странно! — воскликнул Илья, — вот уж я никогда бы не подумал, что землемер или портниха занимаются не-евклидовой геометрией! Впрочем… я и о фонтанах китов тоже не догадался бы.

— Вот то-то и оно! — сердито возразил Радикс. — Имей в виду, кстати, что сам Бельтрами был геодезист, то есть именно землемер. Есть основания думать даже, что и великий Гаусс, который много занимался задачами практического землемерия, натолкнулся на неевклидову геометрию Лобачевского, именно размышляя о своеобразии геодезических задач. Кстати тебе сказать, все споры О «воображаемой» геометрии только тогда и закончились, когда была опубликована наконец перепис-

— 267 —

ка Гаусса, где он откровенно говорит своим друзьям о своих открытиях в области геометрии Лобачевского. Это случилось уже в шестидесятых годах прошлого века, а работы Лобачевского начались с двадцатых годов.

Илюша посмотрел на Радикса и подумал: «Псевдосфера! Вот почему Фавн говорил о псевдокруглом сыре. Понятно».

— Ну, а теперь, — сказал, усмехаясь, Асимптотос, — надо нам вспомнить еще Илюшиного друга — Пифагора.

— Кстати, — подхватил Коникос, — слышал ли ты легенду о «египетском мерном шнуре» с двенадцатью узлами? Греки даже называли египетских землемеров «арпедонапты», то есть «вервиетягатели».

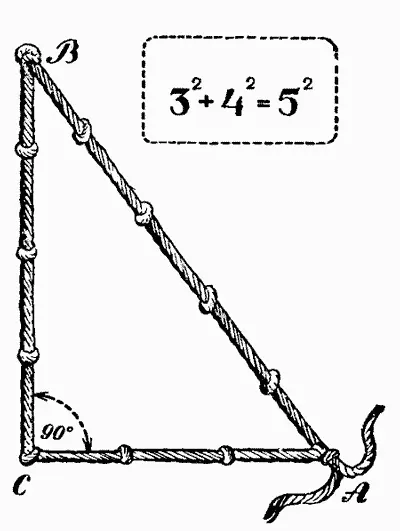
Египетский мерный шнур для построения прямого угла. В точках В и С вбиваются колышки. Получается прямой угол в точке с при одновременном натяжении ВА и СА .

— Нет, — отвечал мальчик.

— Двенадцать, — продолжал Асимптотос, — легко разбить на три слагаемых: три, четыре и пять…

— Пифагоровы числа! — воскликнул Илюша.

— Они самые! Вот поэтому-то при помощи шнура с двенадцатью узлами очень легко построить прямой угол, который нужен и землемеру и строителю. Египтяне знали это правило чуть не за три тысячи лет до вашей эры. У нас здесь есть тоже треугольник — некий волшебно-математический аппарат, который показывает, куда мы попали — в знакомую страну или в незнакомую, где евклидовы и пифагоровы правила не годятся.

— Я как будто догадываюсь. Этот аппарат проверяет, плоская эта поверхность или нет?

— Он не только это проверяет, он еще указывает, далеко ли отклоняется от плоскости данная поверхность и как именно она это делает. А стоит тебе это узнать, и ты сейчас же сообразишь, какая там геометрия годится. Вот и все.

Илюша осмотрел ап-

— 268 —

парат, который представлял собой прямоугольный треугольник, сделанный из оловянного листа, а сбоку был циферблат со стрелкой. В середине стояла большая буква « Е», и на нее указывала стрелка. С одной стороны было написано «Положительная кривизна», а с другой — «Отрицательная кривизна».

Когда Илюша приложил аппаратик к сфере, тот немедленно ответил: «Положительная кривизна». Когда же он приложил аппаратик к стене, то стрелка осталась стоять против буквы « Е», а буква « Е», конечно, напомнила об Евклиде.

— А это что значит? — спросил Илюша. — Ты, Радикс, ведь говорил, что если взять очень большой шар, то там геометрия будет почти такая же, как евклидова.

Значит, чем меньше я буду брать шар, тем будет «более кривая» поверхность с точки зрения этого аппаратика?

— Правильно! — отвечал Радикс. — Если, например, ты на поверхности земного шара будешь брать треугольник со сторонами менее ста километров, ты можешь смело считать его совершенно плоским.

— Ну, а что может значить «отрицательная» кривизна?

Асимптотос с сомнением покачал головой и принес две кривые: одна была эллипсом, другая гиперболой.

— Наша Центрифуга есть поистине дивный аппарат для получения поверхностей вращения.

Затем он взял эллипс и прикрепил его вдоль и посредине (то есть по его большой оси — смотри на картинке!) к стержню, пустил в ход Центрифугу, а потом сиял получившееся тело со стержня.

— Это эллипсоид вращения, — объяснил он.

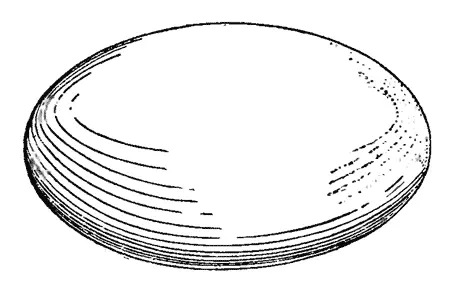
Эллипсоид вращения

— 269 —

Тут он взял две ветви гиперболы и повесил их симметрично в воздухе на равных расстояниях от стержня.

— Простите, пожалуйста! — взмолился Илюша. — Вот когда вы снимаете с Центрифуги конус или эллипсоид, которые, собственно, состоят из ничего, и ставите на пол, ведь это волшебство?