Дэниэл Деннет - Насосы интуиции и другие инструменты мышления [litres]

Итак, вот какой продвинутой наивной антропологией стоит заняться философам, чтобы провести исследование здравого смысла или манифестной картины мира, прежде чем строить свои теории о знании, правосудии, красоте, истине, нравственности, времени, каузации и подобных вещах, чтобы удостовериться, что они анализируют и аргументируют темы, которые действительно значимы для остального мира – как в научном, так и в обывательском представлении. В результате такого систематического анализа появится своеобразный каталог нереформированного концептуального ландшафта, ставящего задачи теоретикам, – если угодно, метафизика манифестной картины мира. Именно здесь философам и нужно установить соответствие с последними инновациями научной картины мира, а потому наличие подробной карты этого народного ландшафта совсем не повредит. Можно сказать, что это вторая половина реформы, которая превратила философию науки из кабинетной фантазии в серьезное партнерство с настоящей наукой, когда философы науки решили, что им действительно нужно познать современную науку изнутри. Размышляя о наших философских задачах с такой позиции, мы видим, что немалая доля неформального труда, лавирования, приведения контрпримеров и подпитки интуиции на страницах философских журналов представляет собой – в лучшем случае – попытку прийти к приемлемому консенсусу об этой территории.

Рассмотрим следующую шахматную задачу [83]. Мат белыми в два хода.

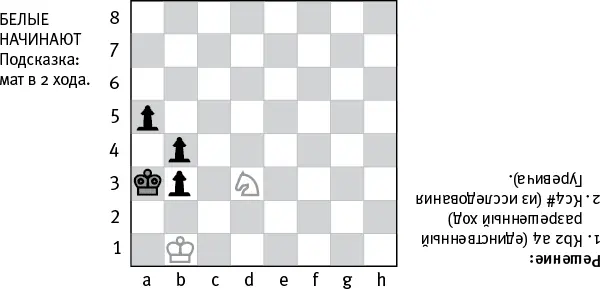
Эта задача была недавно опубликована в Boston Globe и привлекла мое внимание, поскольку я был уверен, что доказана невозможность поставить мат одиноким конем (и королем, конечно). Я ошибался: как недавно заметил в письме ко мне Дэвид Мусяловски, доказано, что нельзя поставить мат, если на доске остались только король противника и ваши король и конь. Тот факт, что утверждение о невозможности поставить мат одиноким конем и королем не является шахматной истиной, представляет собой шахматную истину высшего порядка .

Традиционно философия считается априорной дисциплиной наравне с математикой или хотя бы опирается на априорную методологию, и это имеет свои плюсы и минусы. С одной стороны, это позволяет философам не просиживать часами в лаборатории и не проводить полевых исследований, а также не требует от них знакомства с техниками сбора данных, статистическими методами, географией, историей, иностранными языками, эмпирической наукой и прочими областями знания, что дает им достаточно времени для оттачивания своих философских навыков. С другой стороны, как часто отмечается, философию можно создать из чего угодно, и это не всегда хорошо. Для молодых читателей, подумывающих о карьере в этой сфере – а я надеюсь, такие среди вас есть, – эта глава послужит предупреждением, что свобода и абстрактность философии могут быть ее слабостями. Для неспециалистов эта глава также станет путеводителем по особенностям и ловушкам философии.

Рассмотрим в качестве образца априорной истины шахматную истину. Люди играют в шахматы – и это эмпирический факт. Существует также множество других эмпирических фактов о шахматах, о том, как люди играли в них веками, как часто они использовали красивые резные фигуры, расставленные на инкрустированных досках, и так далее. Никакое знание этих эмпирических фактов не играет незаменимой роли в установлении априорных истин о шахматах, которых также немало. Вам необходимо знать лишь правила игры. Существует ровно двадцать разрешенных первых ходов (шестнадцать ходов пешек и четыре хода слонов); королем и одиноким слоном – а также королем и одиноким конем – не поставить мат одинокому королю, и так далее. Устанавливать эти априорные истины о шахматах порой непросто. Задача доказать, что в шахматах возможно, а что невозможно, весьма сложна, и ошибки вполне вероятны. К примеру, несколько лет назад компьютерная шахматная программа обнаружила матовую сеть – гарантированную или вынужденную победу, – состоящую из более чем двухсот ходов без взятий. В результате оказалась опровергнута устоявшаяся шахматная “теорема” и пришлось менять правила игры. Ранее ничья (пат) объявлялась после пятидесяти ходов без взятий с каждой из сторон, но после обнаружения этой длинной непрерывной матовой сети, приводящей к победе, правило о пате после пятидесяти ходов стало безосновательным. (До того как компьютеры начали играть в шахматы, никто и представить себе не мог, что такая длинная серия ходов вообще может привести к гарантированной победе.) Все это весьма интересно, и многие умные люди посвятили себя изучению системы априорных шахматных истин [84].

Некоторые философские исследовательские проекты – или проблемы, если вам угодно, – напоминают попытку установить шахматные истины. Существует – и редко обсуждается – набор общепринятых правил, а из этих правил выводятся следствия, которые затем формулируются, выставляются на дебаты и корректируются. Пока все понятно. Шахматы – серьезный и важный человеческий артефакт, о котором написано немало ценных трудов. Однако некоторые философские проекты напоминают попытку установить махматные истины. Махматы во всем похожи на шахматы, только король в них может двигаться на две, а не на одну клетку в любом направлении. Я только что придумал эту игру, хотя и не сомневаюсь, что кто-нибудь уже успел ее изучить и выяснить, заслуживает ли она внимания. Вероятно нет. Вероятно, ее называют иначе. Я не стал задаваться этими вопросами, потому что на них можно найти ответы, но это не стоит моего времени и сил. По крайней мере, мне так кажется. Априорных истин в махматах столько же, сколько и в шахматах (целая бесконечность), и установить их столь же нелегко. Это значит, что если люди действительно займутся установлением махматных истин, то ошибок им будет не избежать, а эти ошибки нужно будет исправлять, что откроет целую новую область априорных исследований, область махматных истин высшего порядка , например:

1. Предложенное Джонсом (1989) доказательство махматной истины p несовершенно, поскольку он не учитывает следующей возможности…

2. Утверждение Смита (2002) о несовершенстве доказательства Джонса (1989) предполагает истинность леммы Брауна (1975), которая была недавно поставлена под сомнение Гарфинклем (2002)…

И это не игрушки. При установлении махматных истин высшего порядка можно продемонстрировать выдающиеся способности. Здесь уместно вспомнить афоризм психолога Дональда Хебба:

Если нет смысла браться за работу, нет смысла и делать ее хорошо.