Георг Гегель - Наука логики. Том I. Объективная логика

Рассмотрим сначала первое отношение и возьмем для — долженствующего быть заимствованным из области так называемого приложения — определения того момента, в котором заключается интерес действия, простейший пример кривых, определяемых уравнением второй степени. Как известно, уравнением непосредственно дано в некотором степенном определении отношение координат. Следствиями основного определения являются определения других связанных с координатами прямых линий: касательной, подкасательной, нормальной и т. п. Но уравнения между этими линиями и координатами суть линейные уравнения; те целые, как части которых определены эти линии, суть прямоугольные треугольники, составленные прямыми линиями. Переход от основного уравнения, содержащего степенное определение, к этим линейным уравнениям содержит в себе вышеуказанный переход от первоначальной функции, т. е. от той функции, которая представляет собою некоторое уравнение , к производной функции, которая есть некоторое отношение и притом отношение между известными, содержащимися в кривой, линиями. Связь между отношением этих линий и уравнением кривой и есть то, что требуется найти.

Небезынтересно привести здесь ту историческую справку, что первые открыватели умели указать найденное ими решение лишь совершенно эмпирическим образом, не будучи в состоянии объяснить само действие, оставшееся совершенно внешним. Я ограничиваюсь указанием на Барроу , учителя Ньютона. В своих Lect. opt. et geom., в которых он решает задачи высшей геометрии по методу неделимых, отличающемуся ближайшим образом от особенностей диференциального исчисления, он сообщает, «так как его друзья этого настойчиво просят» (Lect. X), также и свой метод определения касательных. Нужно прочесть у него самого, как он решает эту задачу, чтобы составить надлежащее представление о том, как его указания относительно этого метода носят характер указания о совершенно внешнем правиле , в том же стиле, как излагалось когда-то в учебниках арифметики тройное правило или, еще лучше, так называемая проба арифметических действий девяткою (50). Он чертит те маленькие линии, которые впоследствии были названы приращениями в характеристическом треугольнике кривой линии, и затем в виде простого правила предписывает отбросить как излишние те члены, которые в ходе развертывания уравнения выступают как степени или произведения этих приращений (etenim isti termini nihilum valebunt) (51), а также и те члены, которые содержат величины, определяемые лишь из первоначального уравнения (позднейшее вычитание первоначального уравнения из него же с приращениями), и, наконец, подставить вместо приращения ординаты самую ординату и вместо приращения абсциссы — подкасательную . Нельзя, если дозволительно так выразиться, изложить способ более школьно-педантически; последняя подстановка представляет собою сделанное в обычном диференциальном методе основой определения касательной допущение пропорциональности приращений ординаты и абсциссы ординате и подкасательной; в правиле Барроу это допущение выступает во всей своей наивной наготе. Был найден простой способ определения подкасательной; способы Роберваля и Ферма сводятся к чему-то сходному — метод нахождения наибольших и наименьших значений, из которого исходил последний, покоится на тех же основах и том же приеме. Математической страстью того времени было нахождение так называемых методов , т. е. этого рода правил, и притом делать из них секрет, что было не только легко, но в известном отношении даже нужно, и нужно именно потому, что было легко, а именно потому, что изобретатели находили лишь эмпирически внешнее правило, а не метод, т. е. не нечто, выведенное из признанных начал. Такие так называемые методы Лейбниц воспринял от своего времени; Ньютон также воспринял их от своего времени, а непосредственно — от своего учителя; обобщением их формы и их применимости они проложили новые пути в науках, но, занимаясь этим делом, они чувствовали вместе с тем потребность освободить прием от характера чисто внешних правил и старались дать ему требуемое оправдание.

Анализируя метод ближе, мы увидим, что истинный ход действия в нем таков. Во-первых , степенные определения (разумеется, переменных величин), содержащиеся в уравнении, понижаются, приводятся к их первым функциям. Но этим меняется значение членов уравнения. Поэтому уже нет более уравнения, а возникло лишь отношение между первой функцией одной переменной величины и первой функцией другой переменной. Вместо 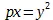мы имеем 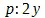или вместо 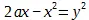мы имеем 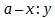, что позднее стали обыкновенно обозначать как отношение 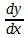. Уравнение есть уравнение кривой, а это отношение, совершенно зависящее от него, выведенное (выше — согласно голому правилу ) из него, есть, напротив, некоторое линейное отношение, которому пропорциональны известные лини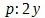и; или 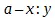сами суть отношения прямых линий данной кривой, а именно отношения координат и параметра; но этим мы еще ничего не узнали . Мы желаем знать о других встречающихся в кривой линиях, что им присуще указанное отношение , желаем найти равенство двух отношений. — Следовательно, является вопрос, во-вторых , какие прямые линии, определяемые природой кривой, находятся в таком отношении? — Но это то, что уже ранее было известно , а именно, что такое полученное указанным путем отношение есть отношение ординаты к подкасательной. Это нашли остроумным геометрическим способом древние; новые же изобретатели открыли только эмпирический прием, как придать уравнению кривой такой вид, чтобы получилось то первое отношение, о котором уже было известно , что оно равно отношению, содержащему в себе ту линию (здесь — подкасательную), которая подлежит определению. Частью это придание уравнению желаемого вида было задумано и проведено методически — диференцирование, — частью же были изобретены воображаемые приращения координат и воображаемый, образованный из этих приращений и такого же приращения касательной характеристический треугольник, дабы пропорциональность отношения, найденного путем понижения степени уравнения, с отношением ординаты и подкасательной была представлена не как нечто эмпирическое, взятое лишь из давно знакомого, а как нечто доказанное. Однако это давно знакомое оказывается вообще (а самым неоспоримым образом в вышеуказанной форме правил) единственным побуждением к допущению — и соответственно, единственным оправданием для допущения характеристического треугольника и указанной пропорциональности .