Георг Гегель - Наука логики. Том I. Объективная логика

Лагранж отбросил эту симуляцию и вступил на подлинно научный путь; его методу мы обязаны тем, что усмотрели, в чем дело, так как он состоит в том, чтобы отделить друг от друга те два перехода, которые следует сделать для решения задачи, и рассматривать и доказывать каждую из этих сторон отдельно. Одна часть этого решения — мы при более близком указании хода действия продолжаем пользоваться как примером элементарной задачей нахождения подкасательной — теоретическая или общая часть, а именно, нахождение первой функции из данного уравнения кривой, регулируется особо; эта часть дает некоторое линейное отношение , следовательно, отношение прямых линий, встречающихся в системе определения кривой. Другая часть решения состоит в нахождении тех линий в кривой, которые находятся в указанном отношении. Это теперь осуществляется прямым путем (Théorie des Fonct. Anal., р. II, chap. II), т. е. не прибегая к характеристическому треугольнику, а именно, не делая допущения о бесконечно малых дугах, ординатах и абсциссах и не давая им определений dy и dx , т. е. членов указанного отношения, и не устанавливая вместе с тем непосредственно значения равенства этого отношения с самими ординатой и подкасательной. Линия (равно как и точка) имеет свое определение лишь постольку, поскольку она составляет сторону некоторого треугольника, и определение точки имеется лишь в треугольнике. Это, скажем мимоходом, есть основное положение аналитической геометрии, которое приводит к координатам, или, что то же самое, в механике к параллелограмму сил, именно поэтому совершенно не нуждающемуся в многочисленных стараниях доказать его. — Подкасательная теперь принимается за сторону треугольника, другими сторонами которого являются ордината и соответствующая ей касательная. Последняя как прямая линия имеет своим уравнением 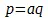(прибавление +b бесполезно для определения и делается лишь ради излюбленной всеобщности); определение отношения 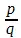есть a , коэфициент величины q , который есть соответственная первая функция уравнения, но который должен вообще рассматриваться лишь как 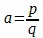, т. е., как сказано, как существенное определение прямой линии, составляющей касательную к данной кривой. Далее, поскольку берется первая функция уравнения кривой, она есть также определение некоторой прямой линии ; далее, так как p , одна координата первой прямой линии, и y , ордината кривой, — берутся как тождественные, так как, стало быть, принимаются, что точка, в которой указанная принимаемая как касательная первая прямая линия соприкасается с кривой, есть вместе с тем начальная точка прямой линии, определяемой первой функцией кривой, то все дело в том, чтобы показать, что эта вторая прямая линия совпадает с первой, т. е. есть касательная, или, выражаясь алгебраически, показать, что так как 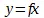и 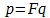, а теперь принимается, что 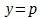, и, стало быть 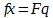, то и 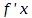тоже 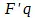. Что употребляемая как касательная прямая и та прямая линия, которая определена из уравнения его первой функцией, совпадают, что эта последняя есть, стало быть, касательная, это показывается с помощью приращения i абсциссы и определяемого через разложение функции приращения ординаты. Здесь, следовательно, также появляется пресловутое приращение; однако следует различать способ, каким оно вводится для только что указанной цели, и разложение функции по этому приращению от вышеупомянутого употребления приращения для нахождения диференциального уравнения и для характеристического треугольника. Употребление, сделанное здесь, правомерно и необходимо; оно входит в круг геометрии, так как геометрическое определение касательной как таковой требует, чтобы между нею и кривой, с которой она имеет одну общую точку, не могло быть другой прямой линии, также проходящей через эту точку. Ибо с принятием этого определения качество касательной или не-касательной сводится к различию по величине , и касательной оказывается та линия, на которую приходится исключительно с точки зрения того определения, которое здесь важно, наибольшая малость . Эта, на первый взгляд, лишь относительная малость не содержит в себе ничего эмпирического, т. е. ничего зависящего от определенного количества как такового; она положена качественно природой формулы, если различие того момента, от которого находится в зависимости долженствующая быть сравниваемой величина, есть различие степени; так как последнее сводится к i и i 2 и так как i , которое ведь в конце концов должно означать некоторое число, следует представлять затем как дробь, то i 2 само по себе меньше, чем i , так что даже представление, что можно приписывать i любую величину , здесь излишне и даже неуместно. Именно поэтому доказательство большей малости не имеет ничего общего с бесконечно малым, и последнее следовательно отнюдь не должно появляться здесь.

Хотя бы только за его красоту и за ныне скорее забытую, но вполне заслуженную славу, которой он пользовался, я хочу здесь еще сказать о декартовом методе касательных; он, впрочем, имеет также отношение к природе уравнений, о которой мы должны будем затем сделать еще дальнейшее замечание. Декарт излагает этот самостоятельный метод, в котором требуемое линейное определение также находится из той же производной функции, в своей и в других отношениях оказавшейся столь плодотворной геометрии (Oeuvres compl. ed. Cousin, tom. V, liv. II, p. 357 ss.), уча в ней о великой основе природы уравнений и их геометрического построения, а тем самым об очень расширенном анализе, о распространении его на геометрию вообще. Проблема получает у него форму задачи — провести прямые линии перпендикулярно к любому месту кривой, чем определяется подкасательная, и т. д. Мы вполне понимаем то чувство удовлетворения по поводу своего открытия, касавшегося предмета всеобщего научного интереса того времени и являвшегося всецело геометрическим, тем самым поднимавшегося так высоко над вышеупомянутыми методами голых правил, которые давались его соперникам, — то чувство, которое он выразил там в следующих словах: «J'ose dire, que c'est ceci le problème le plus utile et le plus général, non seulement que je sache, mais même que j'aie jamais désiré de savoir en géometrie». («Я осмеливаюсь сказать, что это — самая полезная и самая всеобщая геометрическая задача не только из всех тех, которые я знаю, но также и из всех тех, которые я когда-либо желал знать в геометрии»). — Для решения этой задачи он кладет в основание аналитическое уравнение прямоугольного треугольника, образуемого ординатой той точки кривой, к которой должна быть перпендикулярной требуемая в задаче прямая линия, затем ею же самой, нормальной, и, в-третьих, поднормальною, т. е. той частью оси, которая отрезывается ординатою и нормальною. Из известного уравнения кривой в уравнение означенного треугольника подставляется затем значение ординаты или абсциссы; таким образом получается уравнение второй степени (и Декарт показывает, как и те кривые, уравнения которых содержат высшие степени, также сводятся к уравнению второй степени), в котором встречается лишь одна из переменных величин и притом в квадрате и в первой степени, — квадратное уравнение, которое сначала выступает как так называемое нечистое уравнение. Затем Декарт соображает, что если мы представим себе рассматриваемую точку кривой точкой пересечения последней и круга, то этот круг пересечет кривую еще в другой точке и тогда получается для двух тем самым возникающих и неодинаковых x два уравнения с одинаковыми константами и одинаковой формы или же одно уравнение с неодинаковыми значениями x . Но уравнение делается одним уравнением лишь для одного треугольника, в котором гипотенуза перпендикулярна к кривой, т. е. оказывается нормальной, что представляют себе таким образом, что заставляют совпасть обе точки пересечения кривой кругом, и, следовательно, последний становится касающимся кривой. Но тем самым отпадает также и то обстоятельство, что корни x или y квадратного уравнения неодинаковы. В квадратном же уравнении с двумя одинаковыми корнями коэфициент члена, содержащего неизвестные в первой степени, вдвое больше лишь одного корня; это дает нам уравнение, посредством которого мы находим искомые определения. Этот ход решения должен быть признан гениальным приемом истинно аналитической головы, с которым не может сравниться принимаемая всецело ассерторически пропорциональность подкасательной и ординаты якобы бесконечно малым (так называемым) приращениям абсциссы и ординаты.