Нассим Талеб - Рискуя собственной шкурой. Скрытая асимметрия повседневной жизни

Ожидание момента остановки выражается через вероятность успеха при условии отсутствия убытков в прошлом:

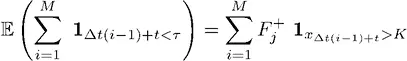
Мы можем записать условие момента остановки в виде непрекращающихся периодов успеха. Пусть ∑ – упорядоченное множество последовательных периодов успеха ∑ ≡ {{F}, {SF}, {SSF}, …, {(M – 1) последовательных S, F}}, где S – успех, а F – неудача за период ∆t, со связанными вероятностями ,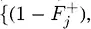

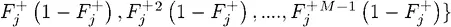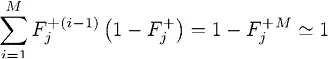
М велико, и, поскольку 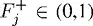, мы можем считать предыдущую формулу почти равенством, так как

Наконец, ожидаемая выплата агенту составит:

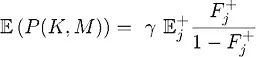
и ее можно увеличить, 1) увеличив 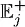и 2) минимизировав вероятность потери 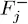, даже если, и это ключевой момент, условия 1) и 2) выполняются за счет m , совокупного ожидаемого от пакета.

Не может не тревожить следующее: поскольку 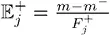, агент не беспокоится об уменьшении совокупной ожидаемой отдачи m , если это проявляется в левой части распределения, m –. В скошенном пространстве ожидаемая отдача агента максимизируется при распределении j с минимальным значением v j (максимальная отрицательная асимметрия). Совокупное ожидание положительной мотивации без шкуры на кону зависит от отрицательной скошенности, а не от m .

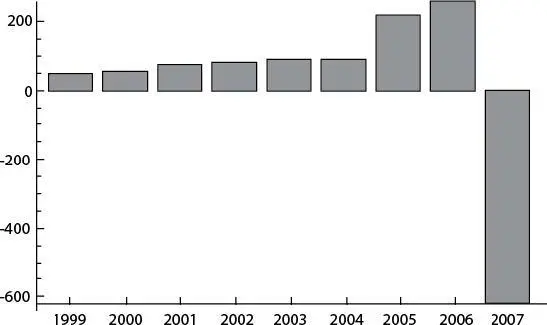
Рис. 8. Indy Mac, компания, потерпевшая банкротство во время кризиса ненадежных кредитов (Taleb 2009). Пример характеризует риски, которые при отсутствии убытков постоянно увеличиваются – вплоть до внезапной катастрофы

Динамическое принятие риска. Если вы принимаете риск – любой риск – повторно, следует учитывать количество моментов риска на продолжительность жизни: такие риски уменьшают оставшийся срок жизни.

Свойства катастрофы. Вероятность катастрофы для отдельного агента лежит в области времени и никак не соотносится с хвостовыми вероятностями пространства состояний (или ансамбля). Ожидания между этими областями не взаимозаменяемы. Таким образом, утверждения о «переоценке» агентами хвостовых событий (включая катастрофу), основанные на оценках пространства состояний, неверны. Многие теории «рациональности» агентов базируются на операторах и/или вероятностных мерах, связанных с ложной оценкой.

Это основной аргумент в пользу стратегии штанги.

Это особый случай, когда мы путаем случайную переменную – и отдачу, выраженную функцией от времени и пути.

В переводе на человеческий язык: никогда не переходите реку, которая в среднем метровой глубины [124] См. спор автора с P. Jorion (1997), а также см. Taleb (2007). .

Рассмотрим чрезвычайно упрощенный пример: дана последовательность независимых случайных переменных 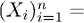(область определения – положительные вещественные числа 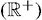. Теоремы сходимости классической теории вероятностей определяют поведение суммы или среднего как lim 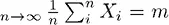по (слабому) закону больших чисел (сходимость по вероятности). Как показано в примере с казино в главе 19, когда n стремится к бесконечности, оно сходится по вероятности к истинной средней отдаче m . Хотя закон больших чисел применим к набору событий i , строго различимых во времени, он допускает (некоторую) независимость – и, конечно, независимость от пути.

Теперь рассмотрим последовательность 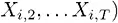, в которой каждому параметру состояния присвоен индекс момента времени t: 0 < t < T . Допустим, что «моменты времени» взяты из точно такого же распределения вероятностей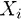: P( ) = P .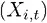

Определим вероятность по времени как эволюцию во времени для отдельного агента i .

В присутствии конечной, то есть необратимой катастрофы всякое последующее наблюдение зависит от некоего свойства предыдущего: то, что происходит в момент t , зависит от t – 1 , то, что происходит в момент t – 1 , зависит от t – 2 и так далее. Мы установили зависимость от пути.

Теперь сформулируем исчезновение эргодичности:

Теорема 1 (неравенство континуума состояний). Пусть и 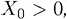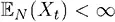– ожидание по пространству состояний для статического начального периода t , а 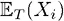– ожидание по времени для всякого агента i , обе формулы получены через слабый закон больших чисел. Тогда: