Нассим Талеб - Рискуя собственной шкурой. Скрытая асимметрия повседневной жизни

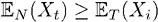
Доказательство:

,

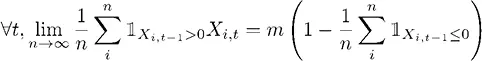где 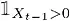– индикаторная функция, требующая выживания в предыдущий период. Границы n для t показывают уменьшение ожидания по времени: .

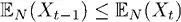На деле мы можем доказать и расхождение.

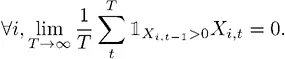
Как можно видеть, если T < ∞ , по закону повторных ожиданий мы получаем неравенство для всех Т .

Мы видим наличие ансамбля рискующих индивидов, ожидающих отдачи m 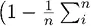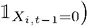, в любой период t , в то время как каждый отдельный рискующий индивид в конце концов гарантированно разорится.

Другие подходы. Мы можем подойти к доказательству с точки зрения более формальной теории меры и показать, что пространственные множества для «некатастрофы» 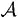не пересекаются, а временные – наоборот. Доказательство основано на том, что для меры :

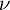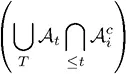не обязательно равно .

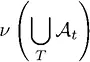Почти ни в одной статье на тему актуарной «переоценки» хвостового риска через опции (см. обзор в Barberis 2003) нет неравенства теоремы 1. Очевидно, статьи основываются на том, что агент принимает только одно решение и проходит через один момент риска. Проще говоря, научные статьи, постулирующие «предвзятость», исходят из того, что агенты более не примут ни одного решения за всю оставшуюся жизнь.

Обычно зависимость от пути – если наблюдается зависимость от катастрофы – устраняется введением функции Х , позволяющей среднему по ансамблю (не зависящему от пути) совпадать по свойствам со средним по времени (оно зависит от пути) – или средним, сопряженным с выживанием. Отличным кандидатом на такую функцию видится натуральный логарифм. Следовательно, 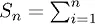log ( X i ) и 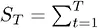log ( X t ) входят в один и тот же вероятностный класс; значит, вероятностная мера одного инвариантна и для другого – это и называется эргодичностью. В этом смысле, анализируя риск и результаты в условиях катастрофы, необходимо использовать логарифмическое преобразование (Peters 2011) или ограниченность левого хвоста (Kelly 1956), максимизируя возможности правого хвоста (Gell-Mann 2016) или ограниченность левого хвоста (Geman et al. 2015).

Мы демонстрируем здесь, что, если не задействовать логарифмическое преобразование (или аналогичную – гладкую – функцию, порождающую –∞ при катастрофе в X = 0 ), ожидания разойдутся. Суть принципа предосторожности – избегать необходимости полагаться на логарифмы и преобразования посредством уменьшения вероятности катастрофы.

В авторитетном исследовании Питерс и Гелл-Манн (2014) показали: Бернулли использовал логарифм не для вогнутой функции «полезности», а (как и в случае критерия Келли) чтобы восстановить эргодичность. Немного истории:

– Бернулли открыл логарифмическое принятие риска под маской «полезности»;

– Келли и Торп вновь открыли логарифм для критерия максимального роста в качестве оптимальной стратегии игрока. Ничего общего с полезностью;

– Самуэльсон отверг логарифм как агрессивную стратегию, не увидев, что возможно полулогарифмическое (или частично логарифмическое) преобразование, применимое к части благосостояния. Многие специалисты по теории решений от Менгера до Эрроу (через Чернова и Самуэльсона) ошибались в том, что касается эргодичности;

– в 1975 году Питмен показал, что броуновское движение при наличии поглощающего барьера в точке 0 и усеченных путей поглощения превращается в трехмерный бесселевский процесс. Дрейф выживших путей составляет 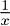, что при интегрировании превращается в логарифм;

– Питерс и Гелл-Манн переоткрыли пользу логарифма для эргодичности и вдобавок обосновали результат Келли – Торпа в строгом физическом аспекте;

– мы с Кирилло (Taleb and Cirillo 2015) обнаружили, что логарифм – уникальное гладкое преобразование, позволяющее создать двойственное распределение. Как следствие, исчезает однохвостная компактная область определения – и можно использовать теорию экстремальных значений;

– можно показать (Briys and Taleb, статья не завершена, частное обсуждение), что логарифмическое преобразование необходимо, если мы хотим избежать катастрофы. На деле это особый случай класса полезности HARA (гиперболическое абсолютное уклонение от риска).

Следствия из упрощенного случая не меняются при переходе к более сложным моделям, таким, как полный стохастический процесс с барьером поглощения. Конечно, в естественной среде может произойти не просто остановка, но прекращение всей предшествующей жизни вообще ( X t может принять крайнее отрицательное значение). Довод Питерса и Гелл-Манна разгадывает также так называемую загадку премии за приобретение акций: вспомним о жирных хвостах (результаты куда сильнее подталкивают эквивалент определенного уровня к катастрофе) и отсутствии взаимозаменяемости времени и ансамбля. Никакой загадки тут нет.

У проблемы есть инвариант в реальной жизни: стохастический процесс типа броуновского движения с поглощающим барьером. Вместо упрощенного примера мы получим для процесса, подверженного риску L , которому соответствует поглощающий барьер снизу, в арифметической версии: