Юрий Дружкин - Очерки теории музыкального моделирования. Книга вторая

Теперь зададим вопрос, можем ли мы найти среди шкал, имеющих значение для музыки, такие, которые не несли бы на себе (в самой своей структуре) печать присутствия человека, культуры и т. п.? Такие шкалы – назовем их условно «суб-музыкальные» – существуют. Одну из них мы уже указали. Это континуальная шкала частот. Континуальная потому, что фактором дискретизации, как правило, выступает человек, его деятельность.

Как правило, чаще всего, но не всегда. И сейчас мы поговорим об одном «чисто объективном» факторе, способствующем выделению особых точек на этой континуальной шкале. Это так называемый обертоновый (или натуральный) звукоряд. Его физическая природа состоит в том, что вибрирующее тело – например, струна – колеблется не только всей своей длиной, но и каждой своей половиной, а также каждой своей третьей частью, четвертой частью, пятой частью и так далее. Самый громкий звук (основной тон) рождается колебанием струны по всей длине. Дальнейшие звуки, порождаемые колебанием частей струны, называются обертонами. Последние, как правило, не слышны в качестве самостоятельных звуков, но в своей совокупности образуют окраску звука – тембр. Впрочем, и в этом превращении обертонового состава звука в его тембр опять-таки мы должны констатировать появление человека и его влияния.

Отношения частот здесь весьма простые: если частоту основного тона принять за x, то частота первого обертона равна 2x, частота второго – 3x, частота третьего – 4x и т. д. Что же касается полутоновой шкалы (темперированного строя), проекция на него натурального звукоряда выглядит более сложно. Если, к примеру, основной тон – это до малой октавы, то первый обертон – до первой октавы, второй обертон – соль первой октавы, третий обертон – до второй октавы, четвертый обертон – ми второй октавы… Более подробную информацию на эту тему легко отыскать в соответствующих источниках.

Исторический процесс развития музыкального искусства – особенно на ранних его стадиях – демонстрировал взаимодействие континуальной и натуральной (обертоновой) шкал, когда неслышимые элементы обертонового ряда как бы «проступали» в виде точек на звуковысотном континууме. Это «проступание» соблазнительно принять за своего рода «естественный» процесс становления различного рода звукорядов, аккордов и т. д. Однако следует все же признать, что без участия человека, его практики, его экспериментов и отбора результатов, так или иначе отвечающих его потребностям, не обошлось и обойтись не могло. Физические, независимые от человека шкалы в определенном смысле действительно существуют. Но их взаимодействие, а также складывание на их основе различных элементов музыкального языка уже обнаруживают участие человека, его психофизиологических особенностей, его практики, его потребностей, человеческого общества и человеческой культуры. Сами по себе, как чисто природные, эти процессы происходить не могут.

Вернемся к рассмотрению шкалы на рис. 2. В ее строении мы выявили две закономерности.

Первая закономерность состоит в том, что она делит (квантует) звуко-высотный континуум на равные отрезки – «полутоны». Каждый полутоновый шаг равен предыдущему полутоновому шагу, так же, как и последующему. Приняв эту закономерность за основу последующих построений, мы можем продолжать движение по полутонам, как в одну, так и в другую сторону, теоретически, до бесконечности. Эту потенциально бесконечную конструкцию мы будем называть «полутоновая прямая».

Понятно, что полутоновая прямая есть теоретическая абстракция, подобная «идеальному газу» или «абсолютно твердому телу». Говоря о ней, мы абстрагируемся от того, что диапазон слышимых звуков ограничен и в реальности никакое движение в бесконечность здесь не представляется возможным. Но мы отвлекаемся от этих естественных ограничений, сосредотачивая внимание на самом способе порождения данной конструкции. Мы также не обращаем внимания на различие белых и черных клавиш, что, фактически, означает переход к тому способу представления, который лежит в основе рис.3. Можно сказать, что разница между этими двумя рисунками нас просто не интересует. Пока не интересует.

Вторая закономерность наглядно видна именно на рис.2, где закономерное чередование белых и черных полос (клавиш) обнаруживает повторяющийся через каждые 12 шагов рисунок. Как мы знаем, этому повторению рисунка соответствует одинаковость названий нот, за которой стоит их перцептивное подобие, т. е. «одинаковость», воспринимаемая на слух. Так, начав, например, в До, мы приходим через 12 шагов по полутонам снова к До. То же самое получится от любого другого звука. Таким образом, мы имеем дело с циклическим процессом, который естественно изобразить в виде круга.

Элементы этого круга (они соответствуют хроматической гамме от До до До) мы будем называть гармоническими элементами (ГЭ), как мы это уже делали в первой части «Очерков теории музыкального моделирования» (глава «Гармоническое исчисление»). Тогда для обозначения гармонических элементов мы использовали римские цифры:

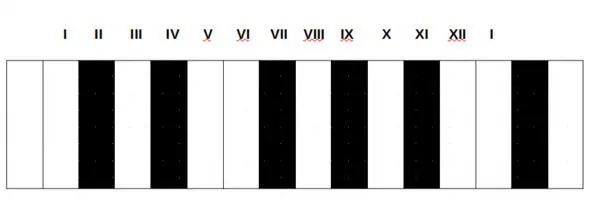
12 гармонических элементов (ГЭ)

Здесь мы видим линейное представление системы из 12 гармонических элементов.

А вот круговое представление этой же системы:

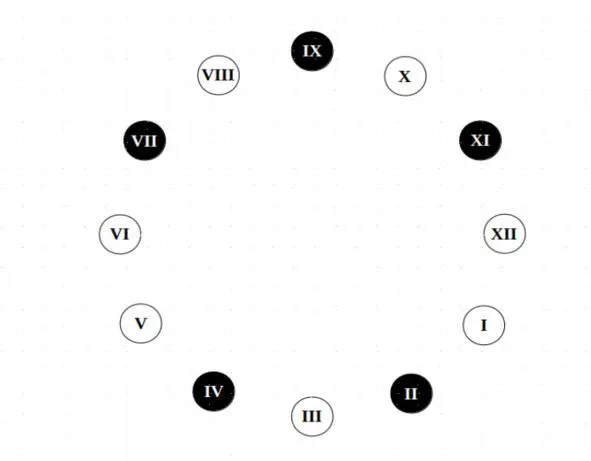
Полутоновый круг

Черные кружочки на рисунке соответствуют черным клавишам фортепианной клавиатуры, образуя пентатонический звукоряд. Белые кружочки соответствуют белым клавишам и образуют семиступенную диатонику. Элементы VI и XII образуют тритон Фа – Си. Если исключить этот тритон их состава «белых» элементов и включить в группу «черных», то семиступенная диатоника превратится в пентатонику, а пентатоника превратится в семиступенную диатонику (например, в фа диез мажорную гамму). У нашего круга из 12 элементов (похожего на циферблат часов) есть 6 диаметров. Один из них (III—IX) является осью зеркальной симметрии (белый-белый, черный-черный):

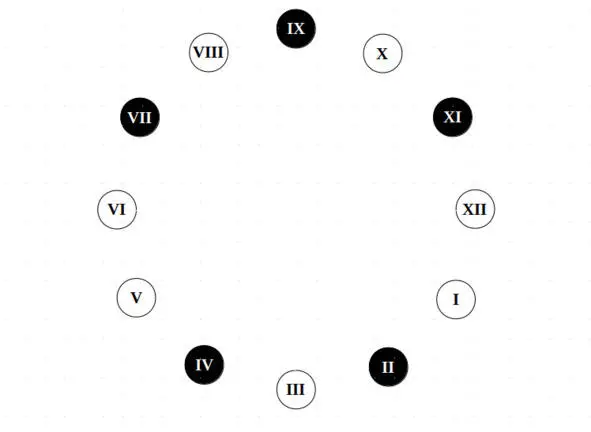
Ось симметрии и асимметрии

Другой диаметр (VI—XII), напротив является осью антисимметрии.

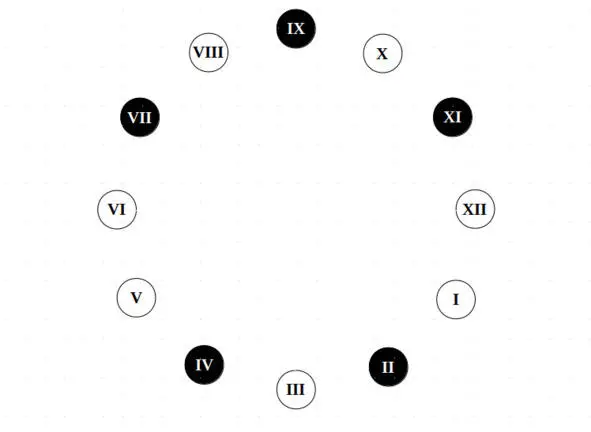
Ось асимметрии

Прочие диаметры такими свойствами не обладают.

Если теперь взять любой из элементов круга и двигаться затем двигаться по часовой стрелке или против, не пропуская ни одного элемента, охватим все без исключения и затем вернемся к исходному. Произойдет это через 12 шагов.