Моррис Коэн - Введение в логику и научный метод

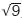, или 3. Если x1, х2, хn являются отклонениями от среднего арифметического из n значений, то σх, т. е. стандартное отклонение, равно

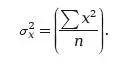
Стандартное отклонение, построенное указанным образом, демонстрирует экстремальные значения отклонений. При возведении отклонений в квадрат наибольшие из них обретают больший вес в общей сумме по сравнению с меньшими отклонениями. Относительно полезности стандартного отклонения нельзя сказать ничего до тех пор, пока не станут известными предположения, сделанные относительно группы значений, для которых оно высчитывается. Однако в целом стандартное отклонение является измерением дисперсии, которое в наименьшей степени подвержено влиянию флуктуаций в выборке по сравнению с другими измерениями. Если распределение в группе является примерно симметричным и если расстояние, равное стандартному отклонению, отграничено с каждой стороны среднего показателя, то около 2/3 всех предметов группы будут находиться внутри отграниченной области. В нашем примере с измерением роста эти отграничения выражаются записью: 66 ± 3. И действительно, около 2/3 величин находится между 63 и 69. Квартильное отклонение

Еще один способ измерения отклонения можно получить в результате расстановки предметов по мере их увеличения и отыскания тех трех значений (item), которые делят общую последовательность на четыре равные части. Эти значения называются «первый квартиль», «второй квартиль» (или медиана) и «третий квартиль». Если Q1 – это первый квартиль, a Q3 – третий, то квартильное отклонение определяется как (Q3 – Q1) / 2. Очевидно, что половина значений группы должна лежать между первым и третьим квартилями. По этой причине квартильное отклонение иногда также называется «вероятностной ошибкой». Если мы используем запись 65,5 ± 2 (где 65,5 является термином, находящимся посередине между первым и третьим квартилем, а 2 – квартальным отклонением), то внутри указанных границ (63,5 и 67,5) будет столько же значений, сколько и снаружи. Иными словами, предполагается, что когда мы произвольно выбираем какие-либо значения группы, то вероятность того, что мы выберем значение, находящееся внутри указанных границ, равна вероятности того, что мы выберем значение за их пределами. Однако выбор термина «вероятностная ошибка» здесь не вполне удачен и сбивает с толку, т. к. в литературе по данной теме этим термином принято обозначать и другие вещи.

Целью всех научных исследований является отыскание значимых отношений внутри изучаемой предметной области. Цель же статистических исследований заключается в том, чтобы облегчить процесс данного открытия и дать возможность выразить отношения между различными группами признаков. Мы собираем статистические данные относительно вопросов, связанных с жизнью, для того чтобы сравнивать такие вещи, как рождаемость, смертность, бедность и т. д., за два различных года. Мы собираем данные о числе несчастных случаев и количестве часов нахождения на рабочем месте на нескольких промышленных предприятиях для того, чтобы установить отношение (если таковое имеется) между этими двумя наборами явлений. Это делается для того, чтобы установить, связаны ли эти обстоятельства причинно-следственной связью или же являются частично или полностью независимыми друг от друга.

Мы уже рассмотрели средние показатели и меры дисперсии, которые обусловливают возможность более или менее точного сравнения групп. Для многих целей рассмотренные статистические числа – это все, что нам нужно. Так, мы можем сравнить доход некоторой общины на протяжении различных лет, используя один из средних показателей и измерения разброса. Иногда становятся полезными процентные отношения. Росла ли численность населения Германии быстрее, чем численность населения Франции между 1900-м и 1910 г.? Увеличение численности населения в процентах в большинстве случаев будет служить мерой такого роста. Существует ли отношение между орлиной формой носа и еврейским происхождением? Недвусмысленный ответ на этот вопрос был получен из данных, согласно которым в достаточно представительных выборках евреев лишь 14 % обладало «характерным еврейским носом».

Однако бывают ситуации, когда никакой из рассмотренных статистических методов не является удовлетворительным. Предположим, мы исследовали несколько сотен листьев с деревьев на предмет соответствия их длины и ширины. Существует ли связь между длиной и шириной листа? На основании наших общих впечатлений мы можем сформировать убеждение о том, что чем длиннее лист, тем он и шире. Однако когда нам приходится рассмотреть множество листьев, то мы уже не можем опираться на поверхностные впечатления, поскольку мы не можем ни запомнить все рассмотренные листы, ни установить между ними значимые отношения. В таком случае мы можем попробовать разложить листья в порядке увеличения их длины, для того чтобы посмотреть, увеличивается ли при этом их ширина. Если две последовательности совпадают, то мы, без сомнения, сможем заключить, что существует определенное отношение между длиной и шириной листа. Если две последовательности совпадают не полностью, а лишь частично, то мы все равно можем подозревать наличие некоторого отношения. Однако нам потребуется некоторая численная мера для соотнесения длин и ширин листьев. Считается, что переменные являются коррелированными, если в последовательности соответствующих примеров этих переменных увеличению или уменьшению в значениях одной из них сопутствует увеличение или уменьшение в значениях другой, будь то в едином направлении или в разных направлениях. Когда значения переменных изменяются в одном направлении (вместе увеличиваются или вместе уменьшаются), корреляция является положительной; когда значения переменных изменяются в противоположных направлениях (одни увеличиваются, а другие уменьшаются), то корреляция является отрицательной.

Существует несколько видов измерения корреляции. Мы рассмотрим только один такой вид, называемый коэффициентом Пирсона. Однако мы не будем рассматривать способ получения этого коэффициента, в силу того что используемый для этих целей аргумент является техническим. Мы просто приведем его определение и продемонстрируем, как он используется. Пусть h1, h2… hn будут значениями переменной h, a w1, w2… wn будут соответствующими значениями переменной w. Это означает, что когда h стоит в значении hlf w стоит в значении и т. д. Далее пусть х1, х2… хn представляют отклонения значений первой переменной от среднего арифметического в n примерах, а у1, у2…уn представляют соответствующие отклонения значений второй переменной. Символы σх и σy будут, как обычно, представлять стандартное отклонение для двух последовательностей. В таком случае коэффициент Пирсона будет обозначаться как