Моррис Коэн - Введение в логику и научный метод

Непосредственное сведение Рассмотрим силлогизм АЕЕ во второй фигуре:

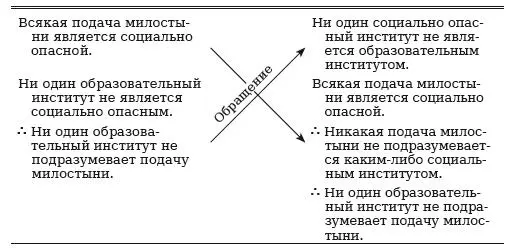
Мы привели силлогизм, эквивалентный исходному справа. Его можно проверить непосредственным образом с помощью принципа dictum. Сведение было осуществлено с помощью перестановки посылок, обращения меньшей посылки и обращения заключения. Следовательно, если мы не сомневаемся в правильности второго силлогизма, у нас не может быть и сомнений в правильности исходного.

Далее рассмотрим модус AII из третьей фигуры. Его можно свести к правильному силлогизму первой фигуры, приведенному ниже справа:

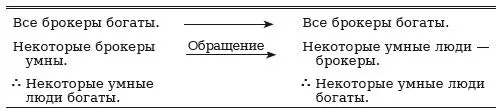
Наконец, модус IAI из четвертой фигуры может быть сведен следующим образом:

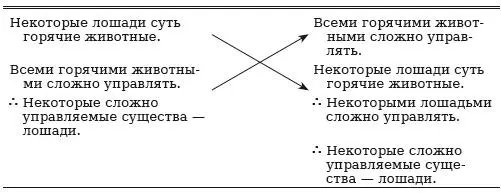
Читатель может заметить, что два силлогизма, содержащие частноотрицательную посылку, АОО во второй фигуре и ОАО в третьей, нельзя свести к первой фигуре только посредством обращения и перестановки посылок. Однако если допустить операцию превращения, то со сведением не возникнет сложностей.

Превращение, однако, не рассматривалось Аристотелем как допустимый способ осуществления сведения. При этом он открыл очень важный логический принцип, являющийся обобщением идеи контрапозиции условных суждений. Прежде чем формулировать данный принцип, проиллюстрируем его.

Допустим, посылки следующего силлогизма являются истинными. Нам нужно доказать, что заключение является истинным с необходимостью.

Некоторые виды стали не являются магнитными. Все виды стали суть металлы.

∴Некоторые металлы не являются магнитными.

Заключение является либо истинным, либо ложным. Если оно ложно, то противоречащее ему суждение «все металлы являются магнитными» истинно. Сочетая это суждение с меньшей посылкой силлогизма, получаем:

Все металлы являются магнитными.

Все виды стали являются металлами.

∴Все виды стали являются магнитными.

Последний силлогизм представляет правильный модус первой фигуры. Но поскольку, согласно гипотезе, обе посылки исходного силлогизма истинны, то заключение второго силлогизма не может быть истинным, поскольку оно противоречит большей посылке исходного силлогизма. Следовательно, большая посылка второго силлогизма не может быть истинной, или, что одно и то же, заключение первого силлогизма не может быть ложным. Следовательно, оно должно быть истинным.

Таким образом, правильность модуса ОАО третьей фигуры доказывается с помощью правильного силлогизма из первой фигуры и принципа, известного как reductio ad absurdum. Правильность модуса АОО из второй фигуры может быть доказана таким же способом. Данный метод можно также использовать и для других модусов.

Проявим теперь принцип reductio ad absurdum в более абстрактной форме. Пусть «р» обозначает суждение «некоторые виды стали не являются магнитными», «q» обозначает суждение «все виды стали являются металлами», а «r» обозначает суждение «некоторые металлы не являются магнитными». Пусть «p′», «q′», «r′» обозначают суждения, противоречащие данным соответственно. Тогда в исходном силлогизме утверждается, что р и q вместе имплицируют r . В символьной форме: ( p . q ) ⊃ r . Мы показали, что суждение, противоречащее r , вместе с q имплицирует суждение, противоречащее р . В символьной форме: ( q . r′ ) ⊃ p′ . Сведение к первому силлогизму зависит от эквивалентности этих двух импликаций. Данная эквивалентность является простым продолжением эквивалентности между условным суждением и противопоставленным ему суждением. Ранее мы показали, что если а и b являются любыми двумя суждениями, то ( а ⊃ b ) ≡ ( b′ ⊃ a′ ). Теперь мы получаем:

[( p . q ) ⊃ r ] ≡ [( q . r′ ) ⊃ p′ ] ≡ [( p . r′ ) ⊃ q′ ].

Итак, принцип опосредованного сведения можно разложить следующим образом: силлогизм – это форма умозаключения, в которой два суждения, p и q, вместе имплицируют третье суждение, r , при этом данные три суждения содержат три, и только три, термина. Однако если мы отрицаем импликацию [( p . q ) ⊃ r ], то мы также должны отрицать и эквивалентную ей вторую импликацию [( q . r′ ) ⊃ p′ ]. Однако эта вторая импликация, как показано в нашем примере, является правильным силлогизмом, представляющим модус Barbara, который нельзя отрицать. Следовательно, также нельзя и отрицать первую импликацию, представляющую силлогизм модуса ОАО из третьей фигуры (т. е. Bocardo). Отрицание правильности модуса Bocardo приводит нас к отрицанию модуса Barbara, а это абсурдно. Если не допускать ослабленные и усиленные формы (т. е. если не предполагать экзистенциальной нагруженности общих высказываний), то сведение позволяет нам усмотреть, что все силлогистические аргументы можно свести к двум формам: одной, в которой обе посылки будут общими суждениями, и второй, в которой обе посылки будут частными суждениями. Первая форма представляет аргумент, в котором оба суждения могут быть всего лишь гипотезами, вторая форма предполагает утверждения относительно факта, которые, в конечном счете, основываются на наблюдении.

Принцип, использующийся в опосредованном сведении, был развит г-жой Кристиной Лэдд-Франклин, что позволило получить новый мощный инструмент проверки правильности любого силлогизма. При рассмотрении данного метода мы отбросим допущение, сделанное нами относительно существования классов, обозначаемых терминами силлогизма. Как следствие, мы исключим ослабленные и усиленные модусы как неправильные.

Рассмотрим правильный силлогизм:

Все музыканты являются гордыми.

Все шотландцы являются музыкантами.

∴Все шотландцы являются гордыми.

Если мы обозначим буквами «S», «М» и «Р» термины «шотландцы», «музыканты» и «гордые индивиды» соответственно и если мы используем результаты анализа того, что утверждается в категорическом суждении, который мы провели в главе IV, то данный силлогизм можно выразить как утверждающий следующее:

Если посылки «все музыканты являются гордыми» и «все шотландцы являются музыкантами» с необходимостью имплицируют заключение «все шотландцы являются гордыми», то из этого следует, что данные посылки несовместимы с суждением, противоречащим заключению. Поэтому три суждения: