Моррис Коэн - Введение в логику и научный метод

Теорема I исключает комбинации АА и AI, а теорема II исключает комбинации IA и ОА. В данной фигуре у нас остается четыре комбинации: АЕ, АО, ЕА и EI, из которых мы получаем шесть правильных модусов. АЕЕ (Camestres), [АЕО], АОО (Baroco), ЕАЕ (Cesare), [ЕАО] и ЕIO (Festino). Модусы, обведенные в круг, являются ослабленными силлогизмами.

Исходя из символьной формы третьей фигуры

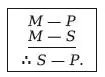
мы можем доказать следующие теоремы.

Теорема I. Меньшая посылка должна быть утвердительной.

Предположим, что меньшая посылка – отрицательная. Тогда заключение будет отрицательным суждением (аксиома 4) и Р, его предикат, будет распределен. Поэтому Р будет распределен и в большей посылке (аксиома 2), и сама большая посылка будет отрицательной. Однако это невозможно (аксиома 3). Поэтому меньшая посылка не может быть отрицательной.

Теорема II. Заключение должно быть частным суждением.

Поскольку меньшая посылка должна быть утвердительным суждением, S в посылках не может быть распределенным.

Поэтому S не может быть распределенным и в заключении (аксиома 2), а само заключение должно быть частным суждением.

Первая теорема исключает комбинации АЕ и АО, и у нас остается шесть комбинаций: AA, AI, EA, EI, IA, OA . Помня о второй теореме, мы получаем шесть правильных модусов: [AAI] (Darapti), AII (Datisi), [ЕАО] (Felapton), ЕIO (Ferison), IAI (Disamis) и ОАО (Bocardo). В этой фигуре нет ослабленных модусов. Два модуса, обведенные в круг, называются усиленными силлогизмами, поскольку то же самое заключение может быть получено, даже если мы заменим суждение одной из посылок подчиненным ему суждением.

С помощью символьного выражения четвертой фигуры

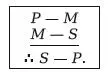
мы можем доказать следующие теоремы.

Теорема I. Если большая посылка является утвердительным суждением, то меньшая посылка является общим суждением.

Если большая посылка является утвердительным суждением, то его предикат, М, нераспределен. Следовательно, М должен быть распределенным в меньшей посылке (аксиома 1), а сама меньшая посылка должна быть общим суждением.

Теорема II. Если одна из посылок является отрицательной, то большая посылка должна быть общим суждением. Если одна из посылок – отрицательное суждение, то заключение является отрицательным (аксиома 4), а его предикат, Р, должен быть распределен. Поэтому Р должен быть распределен и в большей посылке (аксиома 2), а сама она, следовательно, должна быть общим суждением.

Теорема III. Если меньшая посылка является утвердительным суждением, то заключение является частным суждением.

Если меньшая посылка – утвердительное суждение, то его предикат, S, нераспределен. Поэтому S не может быть распределенным и в заключении (аксиома 2) и, следовательно, само заключение должно быть частным суждением.

Первая теорема исключает комбинации AI и AO , вторая – OA . У нас остаются пять комбинаций: AA, AE, EA, IA и EI . С помощью третьей теоремы мы получаем шесть правильных модусов: [ AAI] (Bramantip), AEE (Camenes) , [ AEO] , IAI (Dimaris) , [ EAO] (Fesapo) и EIO (Fresison). AEO является ослабленным силлогизмом, тогда как ААI и EAO – усиленными.

Таким образом, мы обнаруживаем, что всего в четырех фигурах существует двадцать четыре правильные силлогистические формы. В каждой фигуре содержится по четыре правильных модуса. При этом ослабленные и усиленные формы правильны только при допущении экзистенциальной нагруженности, о которой мы четко заявили. Если подобного допущения не делается, то можно получить лишь пятнадцать правильных модусов.

Мы обнаружили правильные модусы посредством исключения всех форм, несовместимых с аксиомами обоснованности, а также с выведенными из них теоремами. Единственным обоснованием правильности выработанных нами форм стала их согласованность с аксиомами. Однако Аристотель, человек, первым написавший о силлогизмах, обосновывал правильные формы иначе. Согласно его подходу, модусы первой фигуры проверялись с помощью применения к ним принципа, известного с тех пор как dictum de omrti et nullo [30] . Данный принцип считался и зачастую до сих пор считается «самоочевидным». Формулировался он по-разному. Одной из таких формулировок была следующая: «Все, что предицируется, в утвердительном или отрицательном суждении, распределенному термину, может также предицироваться и всему, что в нем содержится» (Кейнс). Несложно показать, что принцип dictum эквивалентен аксиомам и теоремам, относящимся к первой фигуре. Однако он не может непосредственно применяться к силлогизмам в других формах. Соответственно первая фигура была названа совершенной, а остальные несовершенными.

Рассмотрим, как с помощью принципа dictum можно проверить правильность силлогизма в модусе Barbara: «Все русские – европейцы; все коммунисты – русские; следовательно, все коммунисты – европейцы». «Европейцы» предицируется в утвердительном суждении распределенному термину «русские», поэтому, согласно принципу dictum, этот термин можно предицировать в утвердительном суждении и «коммунистам», поскольку последний содержится в термине «русские» [31] . Однако силлогизм «все парижане – французы; ни один бостонец не является парижанином; следовательно, ни один бостонец не является французом» не согласуется с принципом dictum. «Французы» предицируется в утвердительном суждении распределенному термину «парижане»; при этом этот термин никак не может предицироваться термину «бостонцы», поскольку последний не содержится в термине «парижане» [32] .

Если мы вместе с Аристотелем будем рассматривать dictum как самоочевидный принцип и если мы вместе с ним решим, что он является единственным самоочевидным принципом, способным определять правильность силлогистических форм, то единственным способом обоснования модусов остальных фигур помимо первой будет демонстрация того, что они предполагают правильные модусы первой фигуры.

Данный процесс проявления связи модусов других фигур с модусами первой фигуры называется «сведением». Существует две разновидности сведения: 1) непосредственное сведение, осуществляющееся посредством обращения суждений, или перестановкой посылок, и 2) опосредованное сведение, требующее либо превращения и контрапозиции суждений, либо формы условного умозаключения, известного как reductio ad absurdum.

Несмотря на то что многие логики считали, что процесс сведения не является необходимым и даже является необоснованным, нет сомнения в том, что в свете той основы, на которой Аристотель развивал свою теорию силлогизма, сведение является неотъемлемой частью этой теории. Однако если учение о силлогизме развивать на иных основаниях, согласно которым первая фигура не считается самой главной, то операция сведения не сможет обладать той важностью, которая приписывается ей в традиционном подходе. Даже принятый нами подход не требует того, чтобы первая фигура рассматривалась как центральная. Ниже мы убедимся, что теорию силлогизма можно развивать, исходя из еще более общих установок. Более того, такие принципы, как dictum, можно выработать для каждой фигуры, и каждый из них будет обладать такой же степенью самоочевидности, как и dictum de omrti. Тем не менее, несмотря на снижение теоретической значимости сведения, оно продолжает представлять ценный логический инструмент. На данном этапе мы покажем, каким образом можно свести к первой фигуре некоторые из модусов других фигур.