Моррис Коэн - Введение в логику и научный метод

Аристотель признавал только первые три фигуры. Введение четвертой фигуры приписывается Галену, и поэтому она, как правило, называется галеновой фигурой. Логики много спорили о том, представляет ли четвертая фигура отдельный тип рассуждения, отличный от типа, представленного в первых трех, и прав ли был Аристотель или нет, не признавая данную фигуру. Если различение фигур осуществляется на основе расположения среднего термина, то, бесспорно, существует четыре разные фигуры. Однако у Аристотеля был иной принцип различения фигур. Этот принцип заключался в ширине, или протяженности, среднего термина по сравнению с другими двумя терминами. Согласно данному подходу, существует лишь три фигуры: средний термин может быть шире одного и уже другого термина, шире обоих терминов или уже каждого из них.

Второй параметр отличия силлогизмов друг от друга – это количество и качество посылок и заключения. Он определяет модус силлогизма. Первый из четырех вышеприведенных силлогизмов соответствует первой фигуре и модусу ЕАЕ. Силлогизм

5. Вся здоровая пища приготавливается из натуральных продуктов.

Все пончики суть здоровая пища.

∴Все пончики приготавливаются из натуральных продуктов.

построен по первой фигуре и модусу АЛА. Таким образом, силлогизмы могут отличаться друг от друга как по фигуре, так и по модусу (например, 1 и 3) или только по фигуре (2 и 4) или только по модусу (1 и 5). Однако не все модусы являются правильными.

Рассмотрим общее число силлогистических форм, правильных и неправильных, с учетом их различия по модусам и фигурам. Поскольку существует четыре типа категорических суждений, то большая посылка, меньшая посылка и заключение могут быть представлены суждениями любого из четырех типов. Следовательно, существует 4x4x4, или 64, силлогистических модуса в каждой фигуре, и 64 х 4, или 256, силлогистических форм в четырех фигурах. При этом большинство из них являются неправильными. Как отыскать правильные формы? Исследовать все 256 форм было бы страшно неудобно. Однако данная процедура вовсе не обязательна, поскольку неправильные формы могут быть исключены посредством применения аксиом и теорем обоснованности.

Запишем каждую возможную комбинацию посылок, где первая буква будет обозначать большую посылку, а вторая – меньшую:

Согласно аксиоме 3, сочетания ЕЕ, ЕО, ОЕ и 00 являются невозможными. Теорема II исключает варианты II, IO, OI , а теорема IV – вариант IE. Следовательно, у нас остается восемь комбинаций посылок, каждая из которых даст правильный силлогизм в некоторых или во всех фигурах: АА, АЕ, AI, АО, ЕА, EI, IA, OA .

Исключенные восемь комбинаций не имеют заключения ни в одной фигуре.

Теперь осталось отыскать правильные модусы для каждой фигуры. Это можно сделать одним из следующих способов:

1. Для каждой фигуры выписать посылки с указанием их количества и качества, согласно каждой из допустимых комбинаций, и путем проверки выявить те комбинации, которые дают обоснованное заключение. Недостаток данного способа в том, что он долгий.

2. Установить специальные теоремы для каждой фигуры и с их помощью исключить неправильные комбинации посылок. Данный метод является изящным, и мы прибегнем именно к нему.

Ниже мы раз и навсегда будем допускать, что обозначаемые терминами классы являются непустыми. Мы исследуем следствия данного допущения. Оно позволит нам осуществлять непосредственные умозаключения с помощью ограничения.

Форма первой фигуры обозначается как

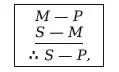
поэтому докажем следующие теоремы.

Теорема I. Меньшая посылка должна быть утвердительной. Допустим, что меньшая посылка – отрицательная. Тогда заключение должно быть отрицательным (аксиома 4), а Р должен быть распределенным. Поэтому Р должен быть распределен и в большей посылке (аксиома 2), а сама большая посылка должна быть отрицательной. Однако обе посылки не могут быть отрицательными (аксиома 3), и, следовательно, меньшая посылка должна быть утвердительной.

Теорема II. Бо′льшая посылка должна быть общим суждением.

Поскольку меньшая посылка должна быть утвердительной, ее предикат М не может быть распределенным. Поэтому М

должен быть распределен в большей посылке (аксиома 1), что, в свою очередь, делает бо′льшую посылку общим суждением.

С помощью специальной теоремы I мы можем исключить комбинации АЕ, АО, а с помощью второй теоремы – комбинации IA и ОА. В первой фигуре обоснованные заключения имеют место только в комбинациях АА, AI, ЕА и EI. Следовательно, шесть правильных модусов – это AAA, [AAI], АII, ЕАЕ, [ЕАО], ЕIO.

Модусы, обведенные нами в круг, называются подчиненными, или ослабленными, модусами, поскольку, несмотря на то что посылки в них предписывают выведение заключения, которое будет общим суждением, действительное заключение, тем не менее, является лишь частным суждением, и поэтому «более слабым», чем могло бы быть. Четырем из этих шести правильных модусов были даны специальные имена, в которых гласные соответствуют символам количества и качества посылок и заключения. Так, модус АЛА обозначается именем «Barbara», All – «Darii», ЕАЕ – «Celarent» и ЕIO – «Ferio». Данные имена были изобретены для формирования мнемонического средства, с помощью которого можно было бы вспомнить различные модусы в каждой из фигур, а модусы второй, третьей и четвертой фигур сводить к модусам первой фигуры. Ниже мы еще вернемся к проблеме сведения.

Форма второй фигуры обозначается как

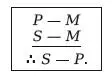
Докажем следующие теоремы.

Теорема I. Посылки должны различаться по качеству.

Если обе посылки являются утвердительными, то средний термин М является нераспределенным в каждой из них. Поэтому одна из посылок должна быть отрицательной (аксиома 1). Обе посылки не могут быть отрицательными (аксиома 3). Поэтому посылки должны различаться по качеству.

Теорема II. Бо′льшая посылка должна быть общим суждением.

Поскольку одна из посылок является отрицательным суждением, заключение также является отрицательным суждением (аксиома 4), и Р, больший термин, должен быть распределенным. Поэтому Р должен быть распределенным и в большей посылке (аксиома 2), а сама посылка должна быть общим суждением.