Арнольд Минделл - Квантовый ум. Грань между физикой и психологией

Минковски смотрел на s и понимал, что это нечто вроде диагонали или гипотенузы – длинной стороны прямоугольного треугольника.

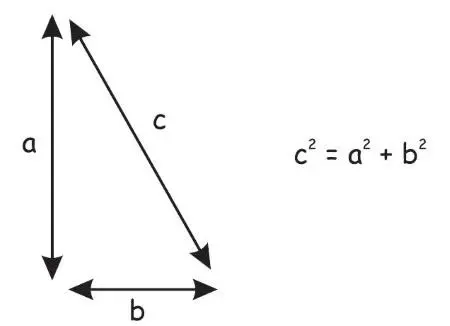
Рис. 25.6. Формула Евклида для прямоугольных треугольников

Минковски смотрел на формулу для прямоугольных треугольников и думал ее сходстве с уравнением для пространства-времени:

s 2 = x 2+ y 2 + z 2– c 2t 2.

Если для простоты заменить координаты x, у и z одной пространственной координатой, скажем x , то мы получим такое уравнение:

s 2= x 2– c 2t 2.

Эта формула пространства-времени похожа на формулу

с 2= a 2 + b 2

для прямоугольного треугольника, где с – это расстояние.

Минковски смотрел на это и думал: «Ммм, это s или пространство-время четырехмерно (три пространственных и одно временное измерение), в то время как тот плоский треугольник двумерен. Как насчет того, чтобы свести s к двум измерениям, поскольку его трудно представлять себе в четырех измерениях. В нашем повседневном трехмерном мире нет ничего похожего на четырехмерную реальность. Физики будущего захотят зрительно представлять себе работу Эйнштейна по теории относительности, но слишком странно, если невозможно зрительно представлять себе то, о чем он говорит».

Поскольку два или три измерения легче представлять, Минковски решил свести четырехмерное гиперпространство, состоящее из x, y, z и t, к двум измерениям. Он приближенно представлял его как плоский треугольник. Это похоже на приближенную оценку площади неровной поверхности части земли. Кривую поверхность трудно измерить, и потому вы приближенно оцениваете ее, считая ее плоской и используя формулу для вычисления площади как произведения длины на ширину.

Стараясь получить зрительное представление нового, четырехмерного мира, Минковски просто переименовал пространства и времена, чтобы иметь с ними дело на равных основаниях. Он обозначил пространственное измерение как x 1( x = x 1), а временное измерение как x 4(-ict = x 4) и получил более простую формулу, имевшую форму прямоугольного треугольника:

s 2= x 1 2+ x 4 2.

Цель всего этого заключалась в том, чтобы представить гиперпространство в терминах обычной реальности. И действительно, приведенная выше четырехмерная формула для пространства-времени выглядит как формула для диагонали прямоугольного треугольника! Если мы можем представить себе треугольник в двух измерениях, то s становится своего рода диагональю.

Математика Минковски достигает упрощения, скрывая мнимое измерение времени. Новый мир Минковски представляет собой сочетание пространственных измерений общепринятой реальности и временных измерений, но перед временем стоит мнимое число (так как -ict = x 4)! Иными словами, очень трудно представить себе измерение времени!

Но мы уже знали с самого начала и без математики, что время обладает пространственными качествами, но движение во времени трудно себе представить. В своем мышлении мы рассматриваем время как пространство. (Например, если бы я спросил: «Как долго вам добираться по шоссе до следующего города?», – вы могли бы ответить: «Около 500 миль».)

Минковски дал измерению x новое название. Это все равно, что называть вас не вашим именем, а именем «пространство 1». Он дал x название x 1! Он также переименовал у, назвав его «пространство 2», или x 2. Точно так же z превратился в x 3. «А что же делать со временем, – думал он, – перед которым стоит тот неудобный знак минус, а именно -c 2t 2»? Он решил, пусть временное измерение будет x 4.

Это было действительно хитро, так как он спрятал знак минус в слагаемом (-c 2t 2), обозначив x 4 2= (-ict) 2и, следовательно, x 4= -ict, так как корень квадратный из минус единицы равен i. (Помните главу 7?) С новыми названиями пространство-время начинает выглядеть немного привычнее:

s 2= x 1 2+ x 2 2+ x 3 2+ x 4 2,

поскольку x = x1, y = x2, z = x3, и -ict = x4, что при y = z = 0 сводится к

s 2= x 2+ x 2.

4. Но подождите, что же случилось со временем 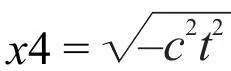? Поскольку квадратный корень из отрицательного числа, вроде -1, равен i, теперь мы имеем x 4= ict.

5. Вычисление пространства-времени. Допустим, что вам не нужны у и z для измерения расстояния, которое планета проходит в одном пространственном измерении х. Тогда мы можем изобразить пространство-время в виде двухмерной карте, которую мы легко себе представляем. Теперь пространство-время представлено в двух измерениях.

Попробуем, например, измерить пространственно-временной интервал планеты, которая прошла 250 миль в пространстве и 1 год по местному времени.

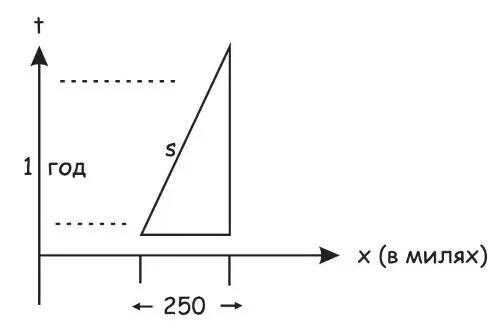
Рис. 25.7. Пространственно-временной график измерения 250 миль и 1 года

Теперь мы могли бы подставить эти величины в приводившиеся выше формулы для х и t и получить s – пространственно-временной интервал, который планета прошла за 1 год земного времени и 250 миль земного пространства. Точно так же мы могли бы даже измерить скорость движения планеты во времени!Смысл нахождения пространственно-временного интервала состоит в том, что эта величина s не зависит от точки зрения, с которой вы ее измеряете.Если бы планета оставалась неподвижной в пространстве, она бы все равно двигалась во времени – в конце концов, она ведь становится старше!

Рис. 25.8. Движение в пространстве-времени, когда нет движения в пространстве

При движении только во времени планета движется в пространстве-времени по прямой линии, поскольку x, у и z вообще не меняются. Существует ли скорость движения во времени? Безусловно, существует. В этом случае скорость движения во времени c = s/t. Как может быть скорость движения вещей во времени? Эта скорость – скорость света. Поэтому, даже не перемещаясь ни на сантиметр с точки зрения данной системы отсчета, вы движетесь сквозь время со скоростью света.

Человек на Луне измеряет x 1' и х 4'. Поскольку

s 2= х 1 2 + х 4 2= х' + x/ 2.

В графическом виде это уравнение показано на рис. 25.9.

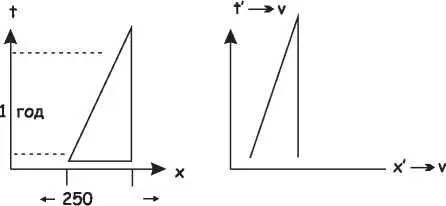
Рис. 25.9 Относительные измерения, видимые на Земле и в движущейся системе