Josep Carrera - Трехмерный мир. Евклид. Геометрия

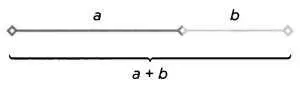
РИС. 14

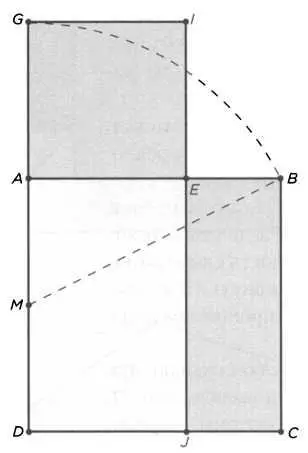
РИС. 15

Ф = (1+ √5)/2 = 1,618033988749894848204586834365638117720309...

Это иррациональное число, то есть число, которое не может быть представлено в виде дроби целых чисел. С геометрической точки зрения для построения золотого отрезка надо разделить данный отрезок АВ в точке Е так, чтобы квадрат с большей стороной АЕ совпал с прямоугольником с меньшей стороной ЕВ и первоначальным отрезком (книга II, предложение 11), как видно на рисунке 15.

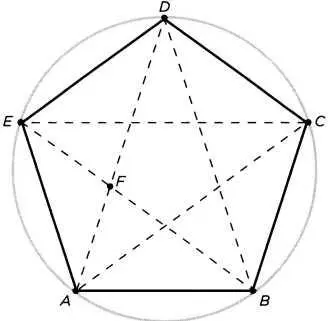
Евклид использовал золотое сечение для промежуточного этапа построения правильного пятиугольника, в частности чтобы получить равнобедренный треугольник, у которого углы в основании были бы в два раза больше угла у вершины. Это удивительное построение можно объяснить, только предположив, что у Евклида уже был пример такого пятиугольника, причем идеального, и что анализируя эту фигуру, он пришел к выводу о необходимости вышеуказанного треугольника. Это еще один пример анализа и синтеза, о которых мы говорили в главе 2. Действительно, при рассмотрении пятиугольника видно, что две диагонали и одна его сторона образуют равнобедренный треугольник, углы в его основании вдвое больше угла у вершины. Диагонали ЕВ и AD пересекаются в точке F, которая делит их в крайнем и среднем соотношении. По всей вероятности, правильный пятиугольник имел особое значение для пифагорейской школы, символом которой, как говорят, была пятиугольная звезда, получаемая путем проведения диагоналей внутри фигуры (непрерывные линии).

При помощи золотого отрезка можно построить прямоугольник, сторонами которого будут первоначальный отрезок АВ и самая длинная часть золотого отрезка, АЕ; поэтому он и называется золотым прямоугольником. На рисунке 15 мы видим, что точка Е делит АВ в крайнем и среднем соотношении. Особенностью этого прямоугольника является то, что он может самовоспроизводиться следующим образом (см. рисунок 16): меньший отрезок BE делит больший отрезок АЕ в крайнем и среднем соотношении и становится таким образом большим отрезком нового деления (точка J делит отрезок ВН(=АЕ) в крайнем и среднем соотношении). Прямоугольник АН является золотым прямоугольником, так же как ЕН, LH и так далее до бесконечности.

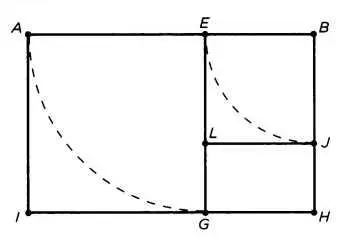
РИС. 16

В заключении «Начал» рассматривается построение Платоновых тел и доказывается, что их существует только пять. В «Тимее» Платон классифицирует природные элементы по пяти телам (см. рисунок 17): тетраэдр он относит к огню из-за его легкости; куб, или гексаэдр, — к земле из-за их стабильности; октаэдр — к воздуху из-за его неустойчивости; икосаэдр — к воде из-за текучести, а додекаэдр — к элементу космоса, пятому, божественному элементу.

РИС. 17

Пять Платоновых тел. Слева направо: тетраэдр, октаэдр, икосаэдр, куб и додекаэдр.

Книга XIII, предложение 18. Кроме упомянутых пяти тел невозможно построить другого тела, заключенного между равносторонними и равноугольными равными друг другу многоугольниками.

Доказательство. Представим, что на листе бумаги стоит точка. Нарисуем вокруг нее 3,4 или 5 равносторонних треугольников, 3 или 4 квадрата и 3 пятиугольника. Если посчитать градусы углов, становится понятно, что другие фигуры невозможны. Следовательно, не могут существовать другие правильные многоугольники, кроме упомянутых выше.

Существует мнение, что золотой прямоугольник встречается во многих произведениях искусства (в частности, в афинском Парфеноне и «Менинах» Веласкеса). Но даже когда искусство прервало классические традиции, как в случае кубизма, прямоугольник остался важным структурным элементом картины. Парфенон — один из самых известных дорических храмов, сохранившихся до наших дней; он был построен между 447 и 432 годами до н.э. Его размеры составляют примерно 69,5 м в длину, 30,9 м в ширину, высота колонн —10,4 м. Храм посвящен богине Афине, которую жители города считали своей покровительницей. А полотно Веласкеса было написано в 1656 году и его размеры — 318 х 276 см. Как видно на рисунках, пропорции их основных элементов образуют золотые прямоугольники. Необходимо уточнить, что хотя эти пропорции и не были результатом специальных построений, все же вряд ли они получились по чистой случайности.

Но существуют ли пять Платоновых тел? Построить первые три относительно легко, а в случае с икосаэдром и додекаэдром все не так просто. Евклид в предложениях с 13 по 17 книги XIII объясняет эти фигуры и вычисляет их стороны

в соответствии с диаметром сферы, в которую они вписаны. Задача сводится к тому, чтобы построить круг, заключающий одну из сторон многоугольника. Это построение является результатом анализа. В качестве примера рассмотрим построение стороны правильного тетраэдра (см. рисунок).

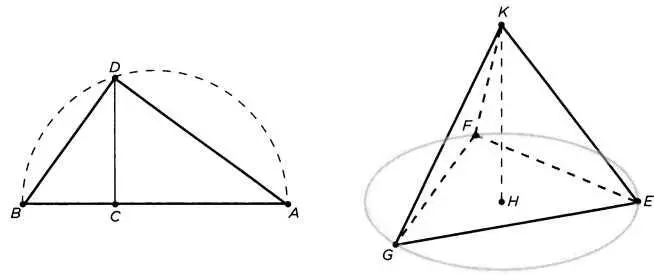
Разделим диаметр АВ круга в точке С так, чтобы АС = 2ВС, Проведем через С прямую, перпендикулярную АВ, пересекающую полукруг ABD в точке D. Проведем окружность с радиусом CD и рассмотрим заключенный в ней равносторонний треугольник. Мы получим три точки: Е, F, G. Проведем через центральную точку Я треугольника EFG прямую НK, перпендикулярную плоскости и равную АС. Соединим К с вершинами Е, F, G и получим тетраэдр. Еще раз отметим, что для этого построения необходимо произвести предварительный анализ, как мы видели в отступлении, посвященном правильному пятиугольнику. Без этого анализа построение невозможно, так как мы не знали бы, какие действия предпринимать.

Францисканский монах и математик Лука Пачоли, итальянец, решает одну из задач евклидовых «Начал». Картина 1495 года, музей и галерея Каподимонте, Неаполь.