Кай Шрайбер - Честная ложь [Почему мы продолжаем верить в то, что портит нам жизнь] [litres]

Этим чисто математическим вопросом озадачился в середине XVIII века британский пастор по имени Томас Байес. Всю жизнь он занимался теологией и вероятностями и обе науки изучал в Эдинбургском университете. Особенно его занимали обусловленные вероятности. Одна из работ пастора на данную тему была публично зачитана его другом в Лондонском королевском научном обществе в 1763 году, спустя два года после смерти автора. Тогда была принята такая форма научной публикации. Работа содержала формулу, которую впоследствии развернул знаменитый математик Пьер-Симон Лаплас. В память о пасторе Томасе она называется теорема Байеса. На заре истории науки она так глубоко проникла в теорию вероятности и в исследования восприятия, что без нее их невозможно представить.

На сегодняшний день восприятие понимается как байесовский процесс и представляет собой постоянную оценку обусловленных вероятностей. Записанная, теорема Байеса кажется соблазнительно простой и поэтичной – особенно если ничего не смыслишь в этой специфической математической лирике.

Теорема Байеса гласит p(T|B) = p(T) × p(B|T) / p(B).

Все ясненько?

До сих пор помню свою первую научную конференцию на ежегодной встрече Общества нейронаук. Это крупное мероприятие, в котором принимают участие более 30 000 ученых со всего мира и где обнародуются новые теории и результаты исследований. В выставочных залах, как осенние стаи перелетных птиц на голых ветвях деревьев, собираются исследователи в области нейронаук, и стоят бесконечные ряды стендов. На каждом из них висят постеры с результатами последних научных исследований отдельных рабочих групп. Дебри таких постеров – это сегодняшний аналог чтений в Лондонском королевском научном обществе.

Стенды сгруппированы по тематикам. Один ряд посвящен изучению освоения языка маленькими детьми, другой – роли кальция в клеточных мембранах синапсов у морских кроликов, а по соседству представлены теоретические выкладки о свойствах искусственных нейронных сетей. Когда продираешься сквозь эти дебри, кажется, что ты заблудился и попал в место, где почти не ориентируешься, – со мной такое случилось, когда я забрел в заросли стендов о молекулярной генетике и биохимии. Рядом с ними группками толпились специалисты в перечисленных областях и обменивались мнениями. Я шел, изумленный и мало что понимающий в их разговорах, а вокруг гудели голоса этого остающегося закрытым для меня мирка.

Однако гораздо больше, чем незнакомые области (где мне просто не хватало знаний, чтобы вступить в разговор и поддержать его), меня впечатлили те группы, где обсуждались известные темы, но на каком-то диковинном языке. Похожие чувства я испытал, когда впервые услышал о приложении байесовской теории к системе восприятия. Количество исследований в этой области растет с каждым годом, о чем свидетельствуют плотно висящие постеры. В конце концов я быстро привык к формулам и математической логике Байеса, но тогда я думал, что чтение странных значков раскроет невидимые трещины в земле, как Vrata od mora [38], и я пройду сквозь подземный мир, о существовании которого и не подозревал.

Все не так печально, но мне придется попросить вас действительно как следует сосредоточиться. Итак, отложите мобильный телефон (конечно, может быть, вы как раз на нем и читаете эту книгу. Тогда не откладывайте). Формула Байеса чрезвычайно важна, а упакованное в нее знание – своего рода отправная точка в познании мира человеком, поэтому каждый должен выделить время, чтобы на примере с монетками проследить и понять ее суть.

Если вы относитесь к числу тех, кого математические формулы повергают в ужас, то можете снова присоединиться к нам в конце следующей главы. Там дается объяснение байесовского правила, и я обещаю, что вы не пропустите ничего принципиально важного для понимания изложенного в книге. Вам лишь придется поверить мне как эксперту на слово касаемо вещей, которые вы смогли бы осмыслить самостоятельно, прочитав главу полностью. Это – справедливое разделение труда и основа всех основ.

Некоторые скорее дадут проткнуть им руку, чем займутся математикой

Однако главный посыл этой книги – всегда требуется немного усилий, когда дело касается реализации основной цели восприятия, а именно, улучшения нашей жизни. В долгосрочной перспективе те, кто избегает этих усилий, причинят вред себе и окружающим. Итак, не бойтесь. Я представляю, как вы себя чувствуете, когда на вас наглыми глазами смотрит голая формула. Дайте мне руку, и я проведу вас через дремучий лес чисел.

Оно стоит того.

Указатель пути в числовых дебрях – условно достоверно – просчитать мошенника – восприятие и предрассудки

Чтобы было легче сориентироваться, прямо на входе в числовые дебри пастора Байеса (Вход свободный!) на большом указателе яркой краской начертана формула:

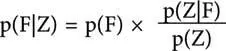
А рядом улыбающийся смайлик. Очень полезно, сразу смекаешь, что к чему.

Что же означают странные знаки в этой диковинной последовательности? Согласно условиям, 4 маленьких «р» – это различные вероятности, а буквы в скобках указывают, какие именно.

«F» – это предположение, что подброшенная монетка была настоящей. «Z» обозначает выпадение решки. Остаются еще странные вертикальные линии. Их следует понимать как «если», вводящее условие вероятности.

p(F|Z) – вероятность того, что играют неподдельной монетой, если она падает решкой вверх. Значение p(F|Z) – это, собственно, цель нашего эксперимента, на основе его мы и будем судить о том, какой была монета. Остаток формулы показывает, как вычислить интересующий нас показатель.

Вторая вероятность в формуле, p(Z|F), – так называемая обратная. То есть вероятность того, что решка выпадает, если монета не поддельная. Как мы уже знаем, она составляет 50 % или 0,5.

Всегда требуется немного усилий, когда дело касается реализации основной цели восприятия, а именно, улучшения нашей жизни. В долгосрочной перспективе те, кто избегает этих усилий, причинят вред себе и окружающим.

Теорема Байеса демонстрирует, что, несмотря на взаимозависимость, обе вероятности не идентичны. Томас Байес и его формула говорят, что мы можем вычислить искомую вероятность из тех, которые нам уже известны. Тогда в зависимости от того, как упадет монета, будет формироваться и наше к ней отношение.

В формуле недостает еще двух выражений – p(F) и p(Z). Это общая вероятность того, что монета настоящая и будет падать решкой вверх. Обе вероятности не имеют вертикальной линии и, значит, ничем не обусловлены. Поскольку в нашем примере у игрока 2 монетки, одна из которых настоящая, а другая поддельная, мы можем легко установить исходное значение p(F). При случайном выборе из двух монет оно составит 50 %: p(F) = 0,5.