Кай Шрайбер - Честная ложь [Почему мы продолжаем верить в то, что портит нам жизнь] [litres]

Теорема Байеса, как мы увидели, позволяет быстро и легко вычислить вероятность участия в игре монетки, неподдельной или специальным образом оцинкованной. Если бы вы пропустили главу о математических дебрях, то вам пришлось бы просто поверить мне на слово. Может быть, я буду еще более убедителен, если скажу, что на мне надет белый халат ученого.

Хотя мы знаем, что в принципе бывают оцинкованные монеты, у нас все же нет достоверной информации о том, в ходу ли они, и уж тем более о том, лежит ли одна из них в кармане нашего фокусника перед торговым центром. Итак, могут быть фальшивые монеты, которые всегда падают только решкой вверх, или только орлом, или как-то иначе, но не с равной долей вероятности. Использовать могут любую из них.

Примечательно, тем не менее, что человеческий мозг по-прежнему во многих сферах остается эффективнее самого лучшего компьютера и по праву считается самой сложной частью организма.

Если наблюдать за монетой, чье поведение совершенно непредсказуемо, со временем у нас все равно сложится некоторое мнение о том, падает ли она случайным образом или нет. Как нам, в этой связи, применить правило Байеса? Теперь надобно вычислять не только вероятность для двух монет, но и вероятность того, что каждая из них может быть фальшивой. Теоретически это, кажется, невозможно, ведь необходимо рассчитать бесконечное множество вещей. Айфону с такой задачей не справиться – аккумулятор раньше разрядится.

Практически же не имеет значения, выпадет решка в 20 % случаев или в 21 %. Ведь подбрасывать монету придется тысячи раз, прежде чем вообще будет заметна разница. Достаточно взять грубо диапазон в 5 %, которые будут откладываться по шкале от 0 (монета никогда не падает решкой вверх) до 100 %, когда всякий раз выпадает решка. К слову, в списке из 21 монеты есть одна подлинная, у которой в половине случаев просто обязана выпадать решка. После броска каждой из них можно рассчитать по формуле Байеса, имеем ли мы дело с таковой. В результате игры с одними монетами эта вероятность будет возрастать, с другими же – падать. В зависимости от этого сформируется и отношение к монете.

До изобретения компьютера никому и в голову не приходило применять теорему Байеса не только для отдельных случаев, но и для целого ряда одновременно происходящих событий. Но для вычислительной машины подобные расчеты не представляют никакой сложности и являются обычными. Как выяснилось, восприятие человеком или животным того или иного явления можно описать, опираясь на теорему Байеса.

О вазах, зайцах и утках

Модель восприятия, при которой наблюдатель учитывает все возможности и к каждой из них применяет теорему Байеса, в исследованиях называют «идеальный наблюдатель». Причем слово «идеальный» не значит, что наблюдатель верит всей получаемой информации. Как мы сами уже убедились, это абсолютно невозможно. В гораздо большей степени «идеальный» значит, что наблюдатель в условиях реальности со всем ее хаосом, неточностями и неоднозначностями может извлечь из представленных данных максимальную пользу.

Это возможно, если он не только находит наиболее вероятное объяснение для наблюдаемого события, но и вместе с тем получает представление о том, насколько хорошо согласовались бы с имеющимися данными прочие его интерпретации. Так получаются, например, инверсионные фигуры, вроде знаменитой иллюзии кролика-утки, описанной философом Людвигом Витгенштейном [43], или вазы Рубина [44]. Здесь конкурируют между собой два вероятных толкования одной картинки. В зависимости от условий наблюдения смотрящий склоняется в сторону одного или другого.

Однако в невинной формулировке «условия наблюдения», как и в теории относительности, заложена бомба. Она окончательно подрывает наше наивное понимание восприятия и являет собой научную основу пристрастных суждений.

Идеальный наблюдатель в действии

Еще раз вспомним теорему Байеса:

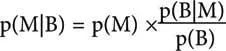
р(M|B) – вероятность того, что наше суждение верно, если некоторое наблюдаемое событие В наступило, вычисляется по двум компонентам. Во-первых, из вероятности, что это суждение соответствует истине р(М) без учета каких-либо данных, и, во-вторых, из фактора, указывающего на то, какова была бы вероятность сделанного наблюдения, если бы М было истинно. В множителе р(М), похрапывая, дремлет страшный циклоп. Без него теорема Байеса не работает и мнение идеального наблюдателя не формируется.

Для большего эффекта повторимся: то, что отражает этот множитель, – это вероятность, что наше суждение верно независимо от самого события. У нас есть для таких вероятностей практичное, короткое и многозначительное понятие. Мы называем их «предубеждениями».

Математика вероятностей непреклонна: без предубеждения невозможно сделать вывод о том, как нам расценивать наблюдаемое событие. Мы видим там в зарослях дрозда? Альбатроса? Ежика? Ундину? Примем ли мы вспышку света в облаках за шар-зонд? За ангела? За НЛО? Звучит неутешительно, но ответ сильно зависит от веры. Ведь, как показывает простая форма байесовского уравнения, очень устойчивое предубеждение может свести на нет любое наблюдение.

Наилучшее умозаключение животного или человека, или идеального наблюдателя, всего лишь прижившееся предвзятое суждение. Это имеет большой смысл – идеального наблюдателя называют так не для забавы, он действительно по-настоящему лучший из всех возможных. В то же время это таит в себе полную катастрофу.

Существенная разница между первым и вторым обнаруживается в том, правомерно ли предвзятое суждение или нет. Если да, то это поможет нам быстрее и лучше установить вероятность. Если нет, то ошибка неминуема. Единственное спасение в том, чтобы вновь и вновь применять теорему Байеса. Перед первым наблюдением мы имеем дело еще с чистым предубеждением. Но после каждого последующего результата мы замещаем это предубеждение суждением, которое складывается из предвзятого мнения и наблюдаемых данных. Если поступает достаточно новой информации, противоречащей привычному отношению к событию, то, по крайней мере, теоретически даже самое устойчивое предубеждение будет в конце концов побеждено.

Возможно, это случится очень быстро. Например, в случае с монетой, если человек убежден, что на обеих ее сторонах отчеканено изображение чьего-то бюста, и вдруг выпадает решка, его мнение тут же изменится. Правда, как правило, побороть крепкие ошибочные представления стоит больших усилий, а тем временем они имеют такой же вес, как истинное суждение.