Юрий Ревич - Занимательная электроника

К микроконтроллерам и Arduino мы еще вернемся — современному радиолюбителю просто нельзя не уметь ориентироваться в ее возможностях, и этой теме мы полностью посвятим последние главы книги. Заметим, что одно из главных удобств такого «индустриального» подхода к радиолюбительству — то, что почти все комплектующие, заранее подобранные по совместимости, можно приобрести в одном месте (примером может служить интернет-магазин «Амперка», ориентированный на Arduino и некоторые другие подобные платформы).

Разумеется, мы не смогли здесь раскрыть и малой доли правил и секретов радиолюбительских технологий. К тому же разные школы радиолюбительского мастерства привыкли к разным технологиям, потому автор не претендует в своих советах на абсолютную истину, рекомендуя лишь то, что его никогда не подводило в течение уже более тридцати лет практики в качестве радиолюбителя и профессионала.

О частотах, периодах, мощности, переменных напряжениях и токах и немного о сигналах

И оба во весь опор помчались в сторону столицы

А.Дюма. Три мушкетера

Электрохимические (гальванические) элементы и аккумуляторы, с которыми мы экспериментировали в главе 1 , являются источниками постоянного напряжения.

Определение «постоянное» не означает, что такое напряжение вообще не меняется. Отнюдь — типичный график зависимости напряжения от времени (так называемые разрядные кривые) для гальванических элементов разных типов приведен на рис. 4.1.

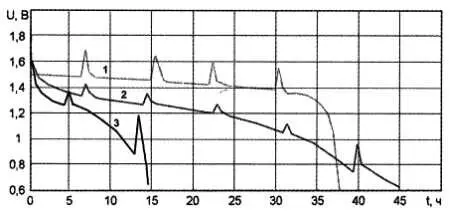
Рис. 4.1. Зависимость напряжения от времени для гальванических элементов при токе нагрузки 100 мА

1— литиевый (в пересчете на напряжение 1,5 В);

2— щелочной типоразмера АА;

3— традиционный марганец-цинковый типоразмера АА.

(По данным И. Подушкина , «Радио», № 2, 2004)

Отметим, что большинство литиевых элементов имеет номинальное напряжение 3 В (для них значение напряжения на графике следует умножить на два), но в последние годы появились и элементы этого типа, аналогичные обычным щелочным. Как видите, зависит напряжение не только от времени — отдельные пики на графиках относятся к моментам, когда нагрузка отключалась, при этом напряжение элемента скачкообразно росло, а затем, при ее подключении, снова падало.

Подробнее об особенностях электрохимических элементов мы поговорим в главе 9 , а сейчас нам важно усвоить, что даже самое-самое постоянное напряжение на деле может быть совсем и не постоянным. Даже для самых качественных источников питания, таких как электрохимические элементы, оно обязательно немножко «гуляет» — в зависимости от тока нагрузки и ее характера. Что же тогда называть переменным напряжением? Строгого определения, как ни странно, не существует — часто приводимое в учебниках выражение «напряжение, которое изменяется с течением времени», как видите, прекрасно подходит и к нашим батарейкам, хотя они являются типичными источниками напряжения постоянного. Поэтому мы договоримся переменными называть такие напряжения или токи, которые изменяются во времени, во-первых, периодически, а во-вторых, делают это «сами по себе», без влияния со стороны нагрузки и других внешних причин.

Слово «периодически» означает, что, начиная с какого-то момента времени, форма графика такой величины повторяется снова и снова (хотя, возможно, и с некоторыми изменениями). Время повтора называется периодом переменной величины. Как вы хорошо знаете из школьного курса физики, наиболее простым и наглядным примером переменной периодической величины является величина, изменяющаяся во времени по синусоидальному закону.

На рис. 4.2 приведен график такой величины в зависимости от времени в условном масштабе. По оси ординат могут быть отложены как напряжение или ток, так и любой другой физический параметр.

Отрезок времени Т есть период изменения, а величина А носит название амплитуды и представляет собой максимальное значение нашей переменной в одном периоде (отметим, что для синусоидального закона минимальное значение — на части графика ниже оси абсцисс — строго равно максимальному). Величина, обратная периоду, обозначается буквой f и носит название частоты (см. формулу на рис. 4.2 вверху). Для нее придумана специальная единица измерения — это хорошо всём знакомый герц (Гц), названный так в честь немецкого физика XIX века Генриха Герца, доказавшего существование радиоволн.

Как следует из определения частоты, размерность герца есть единица, деленная на секунду: 1 Гц= 1/с. Это просто-напросто означает, что колебание с частотой 1 Гц имеет период повторения ровно 1 секунду. Соответственно, 1 кГц (килогерц) означает, что в одной секунде укладывается тысяча периодов, 1 МГц (мегагерц) — миллион периодов и т. п.

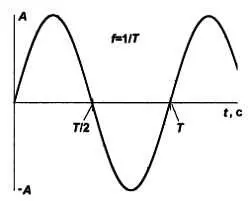
Рис. 4.2. График простого синусоидального колебания

В дальнейшем под «величиной» мы чаще всего будем иметь в виду напряжение (для тока все выглядит аналогично). Математический закон, описывающий поведение синусоидального напряжения ( U ) от времени ( t ), выглядит так:

U= A· sin( 2πft). (1)

Здесь π есть хорошо нам знакомое число «пи», т. е. отношение длины окружности к ее диаметру, равное 3,1415… Произведение 2πf носит специальное название круговая частота и обозначается буквой ω (омега). Физический смысл круговой частоты — величина угла (измеряемого в радианах), пробегаемого нашей синусоидальной кривой за секунду. Поскольку мы обещали не заниматься радиочастотной техникой, то углубляться в дальнейшие абстракции вроде представления переменных колебаний через комплексные числа, где понятие круговой частоты является ключевым, мы не будем — для практических нужд нам пока хватит и более наглядных определений обычной частоты через период.

А что будет, если график немного подвигать вдоль оси абсцисс? Как видно из рис. 4.3, это равносильно признанию того факта, что в нулевой момент времени наше колебание не равно нулю. На рис. 4.3 второе колебание начинается с максимального значения амплитуды, а не с нуля. При этом сдвигаются моменты времени, соответствующие целому и половине периода, а в уравнении (1) появляется еще одна величина, обозначаемая буквой φ (фи) и измеряемая в единицах угла — радианах:

U= A· sin( 2πft+ φ). (2)