И. Хабловски - Электроника в вопросах и ответах

Существуют также другие типы громкоговорителей. Важными параметрами громкоговорителя являются: допустимая акустическая мощность, КПД, сопротивление громкоговорителя как нагрузки схемы, управляющей громкоговорителем.

Верное воспроизведение всего диапазона акустических частот одним громкоговорителем при современном уровне техники оказывается невозможным, и поэтому в устройствах высококачественного воспроизведения применяют комплекты громкоговорителей, содержащие подобранные соответствующим образом громкоговорители для низких и высоких частот. Обычно громкоговорители, хорошо воспроизводящие низкие частоты, значительно больше по размерам, чем громкоговорители для воспроизведения высоких частот.

Преобразователь, превращающий оптическое изображение в электрический сигнал и применяемый в телевизионной камере, работает на принципе использования явления фотоэмиссии или фотопроводимости.

Во втором случае в передающей трубке, называемой видиконом , оптическое изображение, проектируемое объективом на пластинку со слоем фоторезистора, изменяет сопротивление в различных ее местах в зависимости от интенсивности света, падающего в данное место. Увеличение интенсивности света вызывает убывание сопротивления. При проектировании изображения на пластинке возникает определенное распределение потенциала, зависящее от распределения света и теней в проецируемом оптическом изображении. В трубке имеется электронный луч, который направлен на пластинку и перемещается по ней по определенному закону. Перемещаясь, луч попадает на точки с разным потенциалом, что вызывает протекание через пластину тока, значение которого в каждый момент зависит от сопротивления в данной точке, т. е. от количества света, падающего на точку. Таким образом, получают ток, изменяющийся в зависимости от распределения светлых и темных точек пространства.

Преобразование электрического сигнала в оптическое изображение происходит в приемных трубках, называемых кинескопами . Принцип действия кинескопа тот же, что и осциллографических трубок. Электронный луч воздействует на экран, покрытый материалом, светящимся под его воздействием. Интенсивность свечения зависит от тока луча, который в свою очередь зависит в каждый момент от мгновенного значения управляющего трубкой сигнала, полученного от передающей трубки.

Это комбинации, образующиеся в результате соединения электрических элементов. В общем случае определение «цепь» применяется по «отношению» к простым комбинациям элементов, а определение «схема» — к более сложным, однако такое деление строго и последовательно не соблюдается.

Цепи и схемы делятся на разные группы в зависимости от принципа действия, функции, технологии, свойств и т. п. В дальнейшем мы познакомимся с определением и сущностью цепей и схем, называемых линейными и нелинейными, активными и пассивными, логическими и цифровыми, резонансными, связанными, печатными, интегральными и др.

Линейные цепи — это цепи, состоящие только из линейных элементов, т. е. таких, для которых зависимость между напряжением и током является линейной. В общем случае линейными элементами не являются транзисторы, лампы, катушки индуктивности, трансформаторы с сердечником и преобразователи. На практике цепи, содержащие нелинейные элементы и называемые нелинейными, рассматриваются приближенно как линейные, особенно при работе с малыми уровнями сигналов.

Пассивными цепями называются цепи, не содержащие активных элементов, т. е. элементов, повышающих уровень энергии подводимого сигнала, таких как, например, транзистор или лампа.

Это линейная цепь (рис. 2.16, а ), используемая для изменения формы подводимого сигнала. Форма выходного сигнала при возбуждении такой цепи прямоугольным импульсом представлена на рис. 2.16, б . Скорость нарастания фронта выходного сигнала зависит от постоянной времени τ= RCили τ = L/ R. Чем больше постоянная времени, тем сильнее форма выходного сигнала отличается от формы входного сигнала.

Интегрирующую цепь можно рассматривать как фильтр, пропускающий низкочастотные составляющие сигнала и подавляющий составляющие более высоких частот, т. е. как фильтр нижних частот.

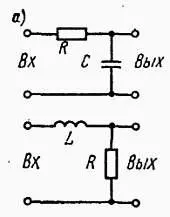
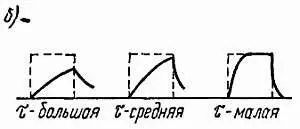
Рис. 2.16. Примеры простых интегрирующих цепей ( а) и форма импульса ( б) на выходе

Это линейная схема (рис. 2.17, а ), используемая для изменения формы подводимого сигнала. При подаче прямоугольного импульса на выходе цепи получают сигнал, форма которого показана на рис. 2.17, б . Изменение формы сигнала тем больше, чем меньше постоянная времени цепи τ= RCили τ = L/ R.

Дифференцирующую цепь можно рассматривать как фильтр, пропускающий высокочастотные составляющие сигнала и подавляющий низкочастотные составляющие, т. е. как фильтр верхних частот.

Рис. 2.17. Примеры простых дифференцирующих цепей ( а) и форма импульса ( б) на выходе

Это цепь, состоящая из катушки индуктивности и конденсатора, соединенных параллельно. Если учесть потери в катушке и конденсаторе как сопротивление R, то такую цепь можно представить в виде, показанном на рис. 2.18, а . Полное сопротивление этой цепи зависит от частоты (рис. 2.18, б ).

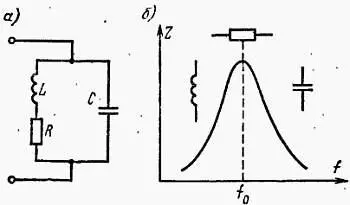
Рис. 2.18. Цепь с параллельным резонансом ( а) и зависимость полного сопротивления цепи ( б) от частоты

Наибольшее значение достигается при частоте собственных колебаний цепи, называемой резонансной частотой и выражаемой формулой

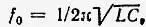
где L— и генри, С— в фарадах, а результат получаем в герцах Резонансное сопротивление (или динамическое) имеет чисто резистивный характер, а его значение рассчитывают по формуле