Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

Упражнение 8.20.Спроектируйте простейший дешифратор, у которого 2-разрядный адрес на выходе будет указывать, какой из четырех входов имеет высокий уровень (все остальные входы должны иметь низкий уровень).

Сумматоры и другие арифметические устройства.На рис. 8.37 изображен 4-разрядный полный сумматор. Он прибавляет 4-разрядное двоичное число А i к 4-разрядному числу В i и вырабатывает на выходе 4-разрядную сумму S i плюс разряд переноса П вых . Для суммирования больших величин сумматоры можно наращивать. Для этой цели предусмотрен вход П вх , на который поступает выходной сигнал переноса от предыдущего (младшего) сумматора.

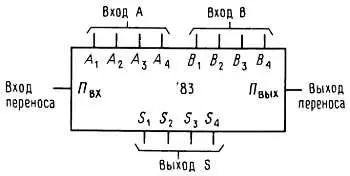
Рис. 8.37. 4-разрядный полный сумматор.

На рис. 8.38 показано, как строится схема для суммирования двух 8-разрядных двоичных чисел.

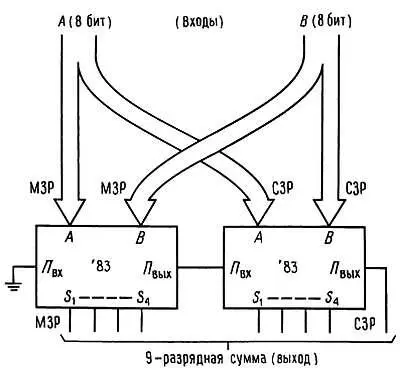
Рис. 8.38. Наращивание сумматора.

Часто в качестве сумматоров используются арифметико-логические устройства (АЛУ). Эти устройства фактически предназначены для выполнения целого ряда различных функций. В частности, 4-разрядная АЛУ `181 (с возможностью расширения для обработки слов большей длины) может выполнять сложение, вычитание, сдвиг двоичных разрядов, сравнение величин и некоторые другие функции. Время выполнения арифметических операций в сумматорах и АЛУ находится в пределах от наносекунд до десятков наносекунд в зависимости от типа логического семейства.

Интегральные умножители выпускаются в конфигурациях 8 бит x 8 бит или 16 бит x 16 бит. Разновидностью умножителей, которые в основном используются для цифровой обработки сигналов, являются так называемые умножители-накопители, которые накапливают сумму произведений. Они также выполняются в размерах 32x32 с 64-битовым произведением плюс несколько дополнительных бит для сохранения суммы от переполнения. Умножители-накопители и умножители выпускаются с временем 25–50 нс; у ЭСЛ-умножителей время меньше — 5 нс (тип.) для умножителей 16x16.

Другим арифметическим устройством, которое используется в цифровой обработке сигналов, является коррелятор, который сравнивает соответствующие биты двух цепочек битов, вычисляя число совпавших битов. Типовой интегральный коррелятор сравнивает два 64-разрядных, которые могут сдвигаться во внутренних регистрах сдвига. Какой-либо набор бит может игнорироваться («маскироваться») в корреляции. Типовые времена составляют 30 нс, т. е. лента бит может тактироваться с частотой 35 МГц, с разрешением 7 бит в корреляции для каждого такта. Вычисляется отклонение (как в цифровом фильтре с КИХ) вместо суммы (с переносом) попарносвязанных произведений двух цепочек целых чисел.

Типичные размеры — целые числа от 4 до 10 бит при длине от 3 до 8 слов (конечно, имеющие возможность расширения). Наиболее сложными арифметическими кристаллами являются процессоры с плавающей запятой, которые осуществляют сравнение, суммирование, умножение, вычисление тригонометрических функций, экспонент и корней. Обычно они используются совместно с определенными микропроцессорами и приспособлены для работы в стандарте, известном как IEED754, который определяет размеры слов (до 80 бит), формат и т. д. Примерами таких устройств (плюс основные микропроцессоры) являются схемы 8087 (80848), 80287 (80286), 80387 (80386) и 68881 (68020/30). Они имеют действительно ошеломляющую производительность в 10 Мегафлопс (миллион операций с плавающей запятой в секунду) или более.

Компараторы.На рис. 8.39 показан 4-разрядный компаратор чисел, который определяет относительные значения чисел А и В и вырабатывает на выходе сигналы результатов сравнения: А < В, А = В и А > В . Входы допускают наращивание для обработки чисел длиной более 4 бит.

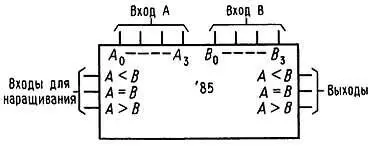
Рис. 8.39. Компаратор.

Упражнение 8.21.Сконструируйте компаратор, используя вентили «исключающее или», который будет сравнивать 4-разрядные числа А и В и определять, когда А = В .

Схема формирования и контроля бита паритета. Это устройство предназначено для выработки паритетного бита, который добавляется к информационному «слову» при передаче (или записи) данных, а также для проверки правильности паритета при восстановлении этих данных. Паритет может быть четным или нечетным (при нечетном паритете для каждого символа общее число битов (разрядов), содержащих 1, нечетно). Например, формирователь паритета 1280 принимает 9-разрядное слово и в соответствии с состоянием управляющего входа вырабатывает на выходе четный или нечетный бит. Конструктивно схема представляет собой набор вентилей «исключающее или».

Упражнение 8.22.Подумайте, как сделать формирователь паритета, используя вентили «исключающее или».

Программируемые логические устройства.Вы можете строить ваши собственные комбинационные (и даже последовательные) логические схемы на кристалле, используя ИС, которые содержат массив вентилей с программируемыми перемычками. Существуют несколько вариантов таких устройств, из которых наиболее популярными являются ПМЛ (программируемая матричная логика — PAL) и ПЛМ (программируемая логическая матрица — PLA). ПМЛ, в частности, стали крайне недорогими и гибкими устройствами, которые должны войти как часть инструмента каждого разработчика. Мы будем описывать комбинационные ПМЛ в следующем разделе.

Некоторые другие незнакомые функции.Существует много других комбинационных схем средней степени интеграции, представляющих несомненный интерес. Например, в семействе КМОП есть схема — «мажоритарная логика», которая говорит, что возбуждена большая часть входов. Имеется также двоично-десятичное устройство дополнения до 9, назначение которого не требует пояснений. Существует схема «барабан-сдвигатель», которая сдвигает входное число на n (задаваемое) разрядов и может наращиваться до любой длины.

К счастью, большинство из проектов цифровых схем не состоит из стряпни безумных устройств на вентилях для реализации сложных логических функций. Однако временами, когда вам нужно связать несколько сложных таблиц истинности, число вентилей может стать слишком большим. Возникает вопрос, нельзя ли найти какой-то другой путь. Таких путей существует несколько. В этом разделе мы кратко рассмотрим, как использовать мультиплексоры и демультиплексоры для реализации произвольных таблиц истинности. Затем мы обсудим в общем более мощные методы, использующие программируемые логические кристаллы, в частности ПЗУ и ПЛМ.