Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

В рассмотренной схеме счетного триггера требование к времени установления будет сохраняться неизменным в течение как минимум 20 нc, предшествующих очередному тактовому перепаду. Может показаться, что при этом нарушается требование к времени удержания, но это не так. Минимальное время распространения сигнала с тактового входа на выход составляет 10 нc, и D-триггер, включенный в счетном режиме, будет иметь неизменное состояние D-входа в течение по меньшей мере 10 нc. Большинство современных устройств вообще не представляют требований ко времени удержания (имеют t уд = 0). Если сигнал на D-входе изменяется на интервале времени удержания, то может возникнуть любопытный эффект, носящий название «метастабильное состояние», при котором триггер не может определить, в какое состояние он должен перейти. Об этом явлении мы вскоре еще упомянем.

Деление на число, большее чем 2.С помощью каскадного соединения счетных триггеров (выход Q каждого предыдущего триггера подключен к тактическому входу последующего) легко получить «делитель на 2 n », или двоичный счетчик. На рис. 8.56 показана схема четырехразрядного асинхронного счетчика и даны его временные диаграммы.

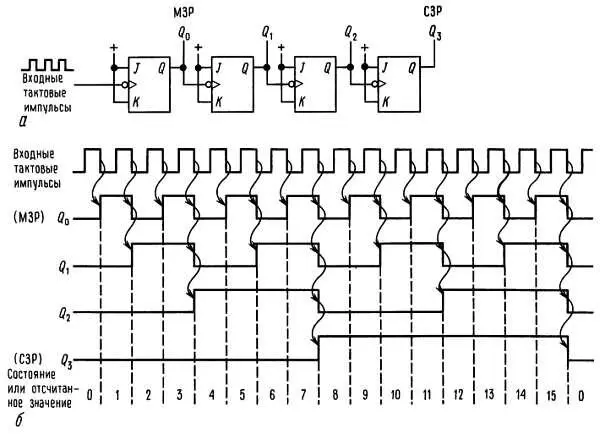
Рис. 8.56. 4-разрядный счетчик.

Заметим здесь, что если выход Q каждого триггера непосредственно действует на тактовый вход следующего, срабатывание триггеров должно происходить по спаду (заднему фронту) сигнала на тактовом входе (показано кружком инверсии). Эта схема представляет собой счетчик-делитель на 16: на выходе последнего триггера формируются прямоугольные импульсы, следующие с частотой, равной 1/16 частоты входного тактового сигнала. Схема называется счетчиком, поскольку информация, присутствующая на четырех входах Q , может рассматриваться как 4-разрядное двоичное число, которое изменяется от 0 до 15, увеличиваясь на единицу с каждым входным импульсом. Этот факт отражает временная диаграмма на рис. 8.56, б , на которой СЗР означает «старший значащий разряд», МЗР-«младший значащий разряд», а изогнутые стрелки, облегчающие понимание, указывают, какими перепадами вызываются изменения сигналов. Этот счетчик, как вы увидите в разд. 8.25 , выполняет настолько важную функцию, что выпускается в виде большого числа модификаций, выполненных в виде однокристальных микросхем, включая такие форматы счета, как 4-разрядный, двоично-десятичный и многоцифровой. Соединяя эти счетчики каскадно и воспроизводя их содержимое с помощью цифрового индикатора (например, светодиодного) можно легко построить схему подсчета каких-либо событий. Если разрешить прохождение импульсов на вход счетчика в течение ровно 1 с, то получится счетчик частоты, который будет воспроизводить значение частоты путем подсчета числа периодов в секунду. В разд. 15.10 приводятся схемы этого простого, но очень полезного устройства. Промышленностью выпускаются однокристальные счетчики частоты, в состав которых входят дополнительно генератор, схемы управления и вывода на индикацию. Триггер такого устройства показан на рис. 8.71.

На практике простейшая схема каскадирования счетчиков посредством соединения каждого выхода Q со следующим тактовым входом имеет некоторые интересные проблемы, связанные с покаскадной задержкой распространения сигнала по цепочке триггеров. По этой причине лучше использовать схему, в которой один и тот же тактовый сигнал подается одновременно на все входы. В следующем разделе мы будем рассматривать эти синхронные тактируемые системы.

После того как мы изучили свойства триггеров, посмотрим, что можно получить, если объединить их с рассмотренной ранее комбинационной (вентильной) логикой. Составленные из вентилей и триггеров схемы, представляют собой наиболее общую форму цифровой логики.

Синхронные тактируемые системы.Мы уже упомянули в предыдущем разделе, что последовательностные логические схемы, в которых для управления всеми триггерами используется общий источник тактовых импульсов, имеют ряд преимуществ. В таких синхронных системах все действия происходят сразу же после возникновения тактового импульса и определяются тем состоянием, которое имеет место непосредственно перед его возникновением. Общая структура подобной системы показана на рис. 8.57.

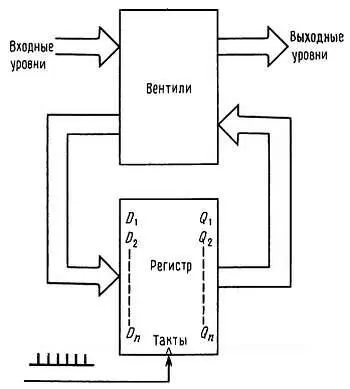
Рис. 8.57. Классическая последовательностная схема: регистры памяти и комбинационная логика. Эту схему можно легко реализовать с использованием однокристальных регистровых ПМЛ (см. разд. 8.27).

Все триггеры объединены в один общий регистр, представляющий собой не что иное, как набор D-триггеров, у которых тактовые входы соединены вместе, а индивидуальные D-входы и выходы Q выведены вовне. Каждый тактовый импульс вызывает передачу уровней, присутствующих на D-входах, на соответствующие выходы Q . Блок, состоящий из вентилей, анализирует состояние выходов регистра и внешних входов, вырабатывает новую комбинацию сигнала для D-входов регистра и выходные логические уровни.

Эта с виду простая схема обладает очень большими возможностями. Рассмотрим пример.

Пример: деление на 3. Попробуем построить схему синхронного делителя на 3 с помощью двух D-триггеров, тактируемых входным сигналом. В этом случае D 1 и D 2 будут входами регистра, Q 1 и Q 2 — eгo выходами, общая тактовая линия будет представлять главный тактовый вход (рис. 8.58).

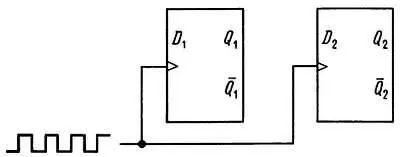
Рис. 8.58.

1. Выберем три состояния:

Q 1 Q 2

______

0 0

0 1

1 0

0 0 (т. е. первое состояние)

2. Определим, что должно быть на выходах комбинационной схемы, для того чтобы получить последовательность этих состояний, т. е. что должно поступать на D-входы, для того чтобы получить требуемые состояния на выходах:

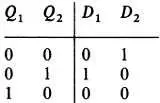
3. Построим вентильную схему, которая, с помощью имеющихся выходов, позволяла бы получить требуемые состояния на выходах. В общем случае можно использовать карту Карно, но для данного простого примера можно сразу увидеть, что D 1 = Q 2, D 2 = ( Q 1 + Q 2 ) ' . Этому соответствует схема на рис. 8.59.

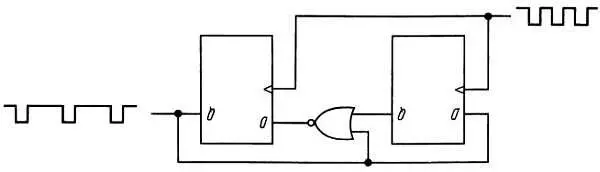
Рис. 8.59. Схема деления на 3.