Пауль Хоровиц - Искусство схемотехники. Том 1 [Изд.4-е]

Итак, одна часть схемы представляет собой усилитель с передаточной проводимостью, коэффициент передачи которого (крутизна) составляет 1 мА/В (1000 мкСм или 1 мСм, а это есть не что иное, как 1/ R Э ). Другая часть схемы представляет собой нагрузочный резистор («усилитель»), преобразующий ток в напряжение. Резистор можно назвать усилителем с передаточным сопротивлением, его коэффициент усиления измеряется в единицах [напряжение/ток], т. е. в единицах сопротивления. В данном случае напряжение покоя (рабочее напряжение) — это U KK , а коэффициент передачи (передаточное сопротивление) равен 10 кВ/А (10 кОм), а это есть не что иное, как R к .

Соединив эти две части последовательно, получим усилитель напряжения, общее усиление которого определяется произведением коэффициентов передачи составных частей. В данном случае: К= g mR к= R к/ R Э= —10 — безразмерная величина, равная отношению [(выходное напряжение)/(входное напряжение)].

Описанный метод очень полезен для анализа усилителей, так как позволяет рассматривать составные части схемы независимо друг от друга. Например, для усилителя с передаточной проводимостью можно оценить величину g m для схем различной конфигурации и для иных элементов, например для полевых транзисторов. Затем можно рассмотреть нагрузку (или часть схемы с передаточным сопротивлением) и оценить, как связан коэффициент усиления с диапазоном изменения напряжения. Если вас интересует общее усиление по напряжению, то его можно определить следующим образом: К U= g mr m, где r m - передаточное сопротивление нагрузки. В конечном счете замена простой активной нагрузки схемой с высоким передаточным сопротивлением позволяет получать для одного каскада усилителя величину коэффициента усиления, равную 10000 и выше. С помощью описанного метода удобно рассматривать каскодный усилитель, с которым вы познакомитесь ниже.

В гл. 4 , где рассматриваются операционные усилители, приведено немало примеров усилителей, на входах и выходах которых действуют напряжения и токи, усилители напряжения, усилители тока, усилители с передаточной проводимостью, усилители с передаточным сопротивлением.

Предельный коэффициент усиления: границы применимости простейшей модели транзистора.В соответствии с нашей моделью коэффициент усиления по напряжению усилителя с общим эмиттером равен — R K / R Э . Что произойдет, если сопротивление R Э будет уменьшаться, стремясь к нулю? Согласно уравнению, коэффициент усиления будет при этом беспредельно возрастать. Однако измерения, выполненные в рассмотренной выше схеме, покажут, что, хотя при постоянном токе покоя, равном 1 мА, коэффициент усиления и растет, при R Э = 0 (эмиттер заземлен) он становится равным всего 400.

Окажется также, что усилитель начнет при этом работать как нелинейный элемент (выходной сигнал не воспроизводит по форме в точности входной), входное сопротивление становится небольшим и нелинейным, а смещение начинает зависеть от температуры. Очевидно, что модель транзистора, которой мы пользовались, несовершенна и ее необходимо дополнить, чтобы она пришла в соответствие с измерениями, описанными выше, и некоторыми другими фактами, на которых мы еще остановимся. Модель, которую мы сейчас рассмотрим, будет достаточно точна и удовлетворит нас в дальнейшем.

Существенную поправку следует внести в правило 4 ( разд. 2.01 ), которое определяет, что I R= h 21ЭI Б. Мы рассматривали транзистор как усилитель тока, вход которого работает как диод. Это приближение является грубым, но для некоторых практических случаев большей точности и не требуется. Однако для того чтобы понять, как работают дифференциальные усилители, логарифмические преобразователи, схемы температурной компенсации и некоторые другие практически полезные схемы, следует рассматривать транзистор как элемент с передаточной проводимостью - коллекторный ток в нем определяется напряжением между базой и эмиттером.

Итак, правило 4 в измененном виде:

4. Если правила 1–3 соблюдены ( разд. 2.01 ), то ток I К связан с напряжением U БЭ следующей зависимостью:

I К= I нас[exp( U БЭ/ U T) — 1]

где U T= kT/ q= 25,3 мВ при комнатной температуре (20 °C), q — заряд электрона (1,60·10 -19Кл), k — постоянная Больцмана (1,38·10 -23Дж/К), Т — абсолютная температура в Кельвинах ( К = °С + 273,16), I нас - ток насыщения транзистора (зависит от T ). Тогда ток базы, который также зависит от U БЭ , можно приблизительно определить так:

I Б = I Кh 21Э

где «постоянная» h 21Э обычно принимает значения от 20 до 1000 и зависит от транзистора, I К, U KЭ и температуры. Ток I нас представляет собой обратный ток эмиттерного перехода. В активной области I К >> I нас и членом — 1 можно пренебречь.

Уравнение для I К известно под названием «уравнение Эберса-Молла». Оно приблизительно описывает также зависимость тока от напряжения для диода, если U T умножается на корректировочный коэффициент m со значением между 1 и 2.

Следует запомнить, что в транзисторе коллекторный ток зависит от напряжения между базой и эмиттером, а не от тока базы (ток базы в грубом приближении определяется коэффициентом h 21Э ). Экспоненциальная зависимость между током I К и напряжением U БЭ точно соблюдается в большом диапазоне токов, обычно от наноампер до миллиампер. На рис. 2.32 приведен график этой зависимости.

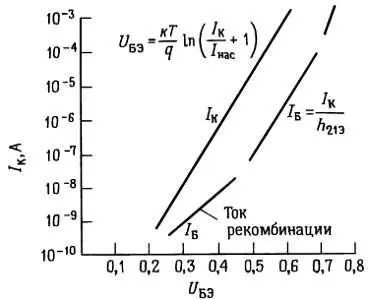
Рис. 2.32. Зависимость базового и коллекторного токов транзистора от напряжения между базой и эмиттером.

Если измерить ток базы при различных значениях коллекторного тока, то получим график зависимости h 21Э от I К (рис. 2.33).

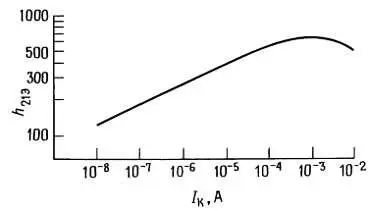
Рис. 2.33. Типичная зависимость коэффициента усиления по току для транзистора ( h 21Э) от коллекторного тока.

Согласно уравнению Эберса-Молла, напряжение между базой и эмиттером «управляет» коллекторным током, однако это свойство нельзя использовать непосредственно на практике (создавать смещение в транзисторе с помощью напряжения, подаваемого на базу), так как велик температурный коэффициент напряжения между базой и эмиттером. В дальнейшем вы увидите, как уравнение Эберса-Молла помогает решить эту проблему.