М. Бабаев - Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
М. Бабаев - Гидравлика краткое содержание
Введите сюда краткую аннотацию
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
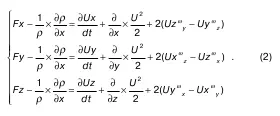
Уравнение Эйлера было получено российским ученым Л. Эйлером в 1755 г., и преобразовано в вид (2) опять же российским ученым И. С. Громекой в 1881 г
Уравнение Громеко (под воздействием массовых сил на жидкость):

Поскольку
– dП = Fxdx + Fydy + Fzdz, (4)
то для компонентов Fy, Fz можно вывести те же выражения, что и для Fx, и, подставив это в (2), прийти к (3).
25. Уравнение Бернулли
Уравнение Громеки подходит для описания движения жидкости, если компоненты функции движения содержат какуююто вихревую величину. Например, эта вихревая величина содержится в компонентах ωx, ωy,ωz угловой скорости w.
Условием того, что движение является установившимся, является отсутствие ускорения, то есть условие равенства нулю частных производных от всех компонентов скорости:
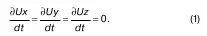
Если теперь сложить
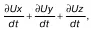
то получим
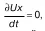
Если проецировать перемещение на бесконечно малую величину dl на координатные оси, то получим:
dx = Uxdt; dy = Uy dt; dz = Uzdt. (3)
Теперь помножим каждое уравнение (3) соответственно на dx, dy, dz, и сложим их:
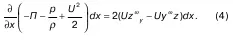
Предположив, что правая часть равна нулю, а это возможно, если вторая или третья строки равны нулю, получим:
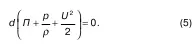
Нами получено уравнение Бернулли
26. Анализ уравнения Бернулли

это уравнение есть не что иное, как уравнение линии тока при установившемся движении.
Отсюда следуют выводы:
1) если движение установившееся, то первая и третья строки в уравнении Бернулли пропорциональны.
2) пропорциональны строки 1 и 2, т. е.

Уравнение (2) является уравнением вихревой линии. Выводы из (2) аналогичны выводам из (1), только линии тока заменяют вихревые линии. Одним словом, в этом случае условие (2) выполняется для вихревых линий;
3) пропорциональны соответствующие члены строк 2 и 3, т. е.
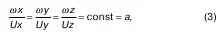
где а – некоторая постоянная величина; если подставить (3) в (2), то получим уравнение линий тока (1), поскольку из (3) следует:
ω x= aUx; ω y= aUy; ω z= aUz. (4)
Здесь следует интересный вывод о том, что векторы линейной скорости и угловой скорости сонаправлены, то есть параллельны.
В более широком понимании надо представить себе следующее: так как рассматриваемое движение установившееся, то получается, что частицы жидкости движутся по спирали и их траектории по спирали образуют линии тока. Следовательно, линии тока и траектории частиц – одно и то же. Движение такого рода называют винтовым.
4) вторая строка определителя (точнее, члены второй строки) равна нулю, т. е.
ω x= ω y= ω z= 0. (5)
Но отсутствие угловой скорости равносильно отсутствию вихревости движения.
5) пусть строка 3 равна нулю, т. е.
Ux = Uy = Uz = 0.
Но это, как нам уже известно, условие равновесия жидкости.
Анализ уравнения Бернулли завершен.
27. Примеры прикладного применения уравнения Бернулли
Во всех случаях требуется определить математическую формулу потенциальной функции, которая входит в уравнение Бернулли: но эта функция имеет разные формулы в разных ситуациях. Ее вид зависит от того, какие массовые силы действуют на рассматриваемую жидкость. Поэтому рассмотрим две ситуации.
Одна массовая сила
В этом случае подразумевается сила тяжести, которая выступает в качестве единственной массовой силы. Очевидно, что в этом случае ось Z и плотность распределения Fz силы Ппротивонаправлены, следовательно,
Fx = Fy = 0; Fz = —g.
Поскольку – dП = Fxdx + Fydy + Fzdz, то – dП = Fzdz,окончательно dП = —gdz.
Интегрируем полученное выражение:
П = —gz + C, (1)
где С – некоторая постоянная.
Подставив (1) в уравнение Бернулли, имеем выражение для случая воздействия на жидкость только одной массовой силы:

Если разделить уравнение (2) на g (поскольку оно постоянное), то

Мы получили одну из самых часто применяемых в решении гидравлических задач формул, поэтому следует ее запомнить особенно хорошо.
Если требуется определить расположение частицы в двух разных положениях, то выполняется соотношение для координат Z 1и Z 2, характеризующие эти положения
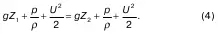
Можно переписать (4) в другой форме
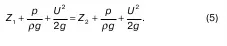
28. Случаи, когда массовых сил несколько
В этом случае усложним задачу. Пусть на частицы жидкости действуют следующие силы: сила тяжести; центробежная сила инерции (переносит движение от центра); кориолисовая сила инерции, которая заставляет частицы вращаться вокруг оси Z с одновременным поступательным движением.
В этом случае мы получили возможность представить себе винтовое движение. Вращение происходит с угловой скоростью w. Нужно представить себе криволинейный участок некоторого потока жидкости, на этом участке поток как бы вращается вокруг некоторой оси с угловой скоростью.
Частным случаем такого потока можно считать гидравлическую струю. Вот и рассмотрим элементарную струйку жидкости и применим в отношении к ней уравнение Бернулли. Для этого поместим элементарную гидравлическую струю в координатную систему XYZ таким образом, чтобы плоскость YOX вращалась вокруг оси O Z.
Будем считать, что U – местная скорость жидкости во вращающейся плоскости YOX. Пусть
Fx 1= Fy 1= 0; Fz 1=—g —
составляющие силы тяжести (то есть ее проекции на оси координат), отнесенные к единичной массе жидкости. К этой же массе приложена вторая сила – сила инерции ω 2r, где r – расстояние от частицы до оси вращения ее компоненты.
Читать дальшеИнтервал:
Закладка:






