М. Бабаев - Гидравлика
- Название:Гидравлика
- Автор:
- Жанр:
- Издательство:Конспекты, шпаргалки, учебники «ЭКСМО»b4455b31-6e46-102c-b0cc-edc40df1930e
- Год:2008
- Город:Москва
- ISBN:978-5-699-24848-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
М. Бабаев - Гидравлика краткое содержание
Введите сюда краткую аннотацию
Гидравлика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
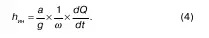
Окончательно уравнение Бернулли для потока, получение которого и являлось задачей рассматриваемого вопроса имеет следующий вид:

Что касается (5), то оно получено из (4) с учетом того, что dQ = wdu; подставив dQ в (4) и сократив ω, приходим к (6).
Отличие hин от hпр прежде всего в том, что оно не является необратимым. Если движение жидкости с ускорением, что значит dυ/t > 0, то h ин> 0. Если движение замедленное, то есть du/t < 0, то h ин< 0.
Уравнение (5) связывает параметры потока только в данный момент времени. Для другого момента оно может уже оказаться не достоверным.
36. Ламинарный и турбулентный режимы движения жидкости. Число Рейнольдса
Как нетрудно было убедиться в вышеприведенном опыте, если фиксировать две скорости в прямом и обратном переходах движения в режимы ламинарное → турбулентное, то
υ 1≠ υ 2
где υ 1– скорость, при которой начинается переход из ламинарного в турбулентный режим;
υ 2– то же самое при обратном переходе.
Как правило, υ 2< υ 1. Это можно понять из определения основных видов движения.
Ламинарным (от лат. lamina – слой) считается такое движение, когда в жидкости нет перемешивания частиц жидкости; такие изменения в дальнейшем будем называть пульсациями.
Движение жидкости турбулентное (от лат. turbulentus – беспорядочный), если пульсация местных скоростей приводит к перемешиванию жидкости.
Скорости перехода υ 1, υ 2называют:
υ 1– верхней критической скоростью и обозначают как υ в. кр, это скорость, при которой ламинарное движение переходит в турбулентное;
υ 2– нижней критической скоростью и обозначают как υ н. кр, при этой скорости происходит обратный переход от турбулентного к ламинарному.
Значение υ в. крзависит от внешних условий (термодинамические параметры, механические условия), а значения υн. кр не зависят от внешних условий и постоянны.
Эмпирическим путем установлено, что:
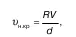
где V – кинематическая вязкость жидкости;
d – диаметр трубы;
R– коэффициент пропорциональности.
В честь исследователя вопросов гидродинамики вообще и данного вопроса в частности, коэффициент, соответствующий uн. кр, называется критическим числом Рейнольдса Re кр.
Если изменить V и d, то Re крне изменяется и остается постоянным.
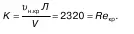
Если Re< Re кр, то режим движения жидкости ламинарный, поскольку υ < υ кр; если Re > Re кр, то режим движения турбулентный из-за того, что υ> υ кр.
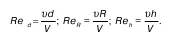
37. Осредненные скорости. Пульсационные составляющие
В теории турбулентного движения очень многое связано с именем исследователя этого движения Рейнольдса. Рассматривая хаотическое турбулентное движение, он представил мгновенные скорости, как некоторые суммы. Эти суммы имеют вид:
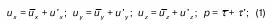
где u x, u y, u z– мгновенные значения проекций скорости;
p, τ – то же самое, но для напряжений давления и трения;
черта у величин наверху означает, что параметр усреднен по времени; у величин u′ x, u′ y, u′ z, p′, τ′ черта сверху означает, что имеется в виду пульсационная составляющая соответствующего параметра («добавка»).
Осреднение параметров по времени осуществляется по следующим формулам:
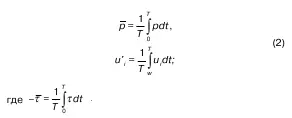
– интервал времени, в течение которого проводится осреднение.
Из формул (1) следует, что пульсируют не только проекции скорости, но и нормальные р ик асательные τ напряжения. Значения усредненных во времени «добавок» должны быть равны нулю: например для х-ой компоненты:

Интервал времени Т определяют достаточным, чтобы при повторном осреднении значение «добавки» (пульсирующей составляющей) не изменилось.
Турбулентное движение считается неустановившимся движением. Несмотря на возможное постоянство осредненных параметров, мгновенные параметры все же пульсируют. Следует запомнить: осредненная (по времени и в конкретной точке) и средняя (в конкретном живом сечении) скорости – не одно и то же:

где υ= Q/w;
Q – расход жидкости, которая течет со скоростью υ через w.
38. Средне квадратичное отклонение
Принят стандарт, который называется среднеквадратическим отклонением. Для х

Чтобы получить формулу для любого параметра «добавки» из формулы (1), достаточно заменить u xв (1) на искомый параметр.
Среднеквадратичное отклонение можно относить к следующим скоростям: усредненная местная скорость данной точки; средняя по вертикали; средняя поживому сечению; максимальная скорость.
Обычно максимальная и средняя по вертикали скорости не используются; используются две из вышеперечисленных характерных скорости. Кроме них, используют также динамическую скорость

где R– гидравлический радиус;
J – гидравлический уклон.
Среднеквадратичное отклонение, отнесенное к средней скорости, есть, например, для х-ой компоненты:

Но лучшие результаты получаются, если среднеквадратичное отклонение относить к u x, т. е. динамической скорости, например

Определим степень (интенсивность) турбулентности, как называют величину e
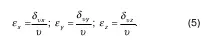
Однако лучшие результаты получаются, если за масштаб скорости (то есть за характерную скорость) взять динамическую скорость u x.
Еще одним свойством турбулентности является частота пульсаций скорости. Средняя частота пульсации в точке с радиусом r от оси потока:
Читать дальшеИнтервал:
Закладка:






